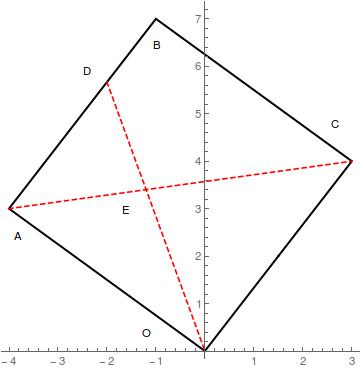
Painful vector problem (please see below - thank you!!). Can you find lambda?
#OABC# is a square with #A# and #C# having position vectors of #a = -4i + 3j# and #c = 3i + 4j# .
#OB = -i + 7j#
#AC = 7i + j#
#OD = -2i + 17/3j# where #D# is a point along the line #AB# , such that #BD = 1/3BA# .
#OD# intersects with #AC# at a point #E# such that #OE = (1-lambda)OA + lambdaOC# .
Find the value of #lambda# .
Find the value of
1 Answer
Explanation:
and now
also
Solving now
we have
Now
with
then solving
we obtain
and finally from