Physics help ??
- An applied force of 109 N is used to accelerate an object to the right across a frictional surface. The object encounters 19.4 N of friction. The object weighs 88.5 N. Calculate the (a) normal force, (b) the net force, (,c) coeficcient of friction (mu, µ), (d) the mass and (e) the acceleration.
- An applied force of 109 N is used to accelerate an object to the right across a frictional surface. The object encounters 19.4 N of friction. The object weighs 88.5 N. Calculate the (a) normal force, (b) the net force, (,c) coeficcient of friction (mu, µ), (d) the mass and (e) the acceleration.
2 Answers
See below.
Explanation:
We are given:
-
#abs(vecF_"applied")=109"N"# -
#"weight" = 88.5"N"# -
#abs(vecf)=19.4"N"#
a.) Find the normal force.
Let's start with a force diagram.
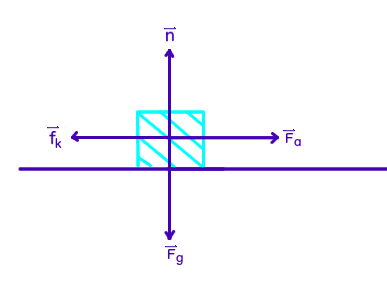
where
Let's define to the left and downward as negative directions. We can then write statements of the net force as follows:
#F_"net, x"=sumF_x=F_a-f_k=ma_x#
#F_"net, y"= sumF_y=n-F_g=ma_y#
Since the object does not accelerate vertically (does not move up or down relative to the horizontal), we have:
#n-F_g=0#
#=>n=F_g#
Since
We are given the object's weight, which in this case is the gravitational force, and so the normal force is given by
b.) Find the net force.
We can refer to our net force statements from part a.
We know that for the net force parallel we have
Then
c.) Find the coefficient of friction.
We know that the force of friction is given by
#mu=f/n#
#=>mu=19.4/88.5#
#=>color(blue)(mu=0.219)#
d.) Find the mass.
As discussed above, we are given the weight of the object, which is equivalent to the force of gravity acting on the object. Therefore we know that
#=>m=(88.5"N")/g#
#=>m=(88.5"N")/(9.81"m"//"s"^2)#
#=>color(blue)(m~~9.02"kg")#
e.) Find the acceleration.
We have established that there is no acceleration in the y-direction. Therefore, all acceleration experienced by the object is parallel to the motion (x-direction). We can find the acceleration using Newton's second law.
We found above that
We found the mass in part b and the net force in part b, so we have:
#=>a_x=(F_a-f_k)/(m)#
#=>a_x=(89.6"N")/(9.02"kg")#
#=>color(blue)(a=9.83"m"//"s"^2)#
Frictional force (
Here,
And,
So,
Net force(
So,acceleration of the object is


