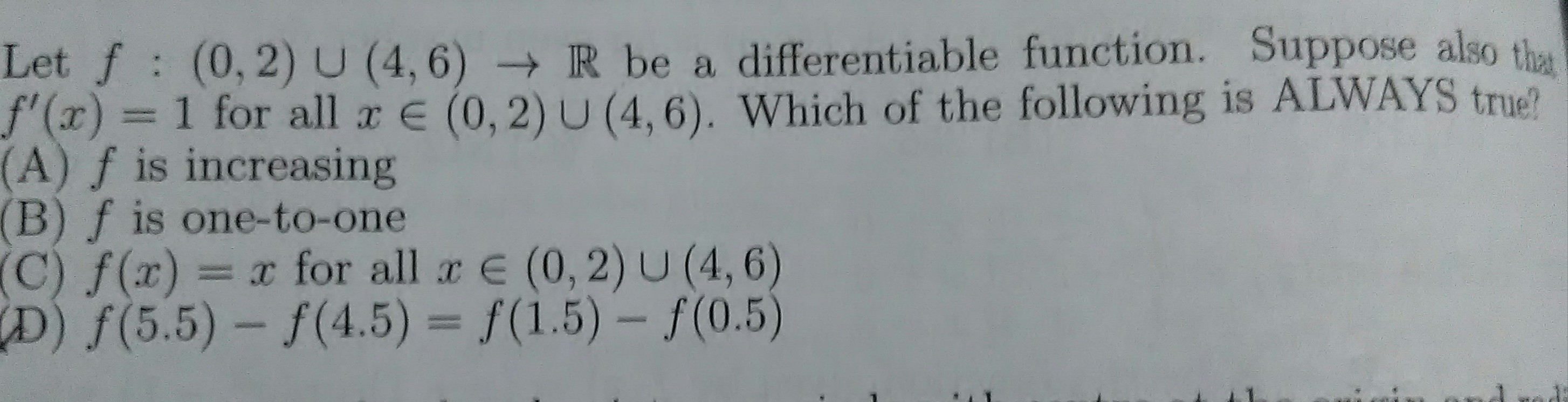#f# is differentiable on each of #(0,2)# and #(4,6)#.
Since differentiability implies continuity, #f# is also continuous on each of the open intervals.
So, for any interval #[a,b]# entirely within one of these open intervals, we can apply the Mean Value Theorem
#f# is continuous on #[a,b]# and
#f# is differentiable on #(a,b)#
Therefore, there is a #c# in #(a,b)# such that
#f(b)-f(a) = f'(c)(b-a)#.
Furthermore, since #f'(c) = 1#, we see that
So, for any interval #[a,b]# entirely within one of these open intervals,
#f(b)-f(a) = (b-a)#.
Therefore,
#f(5.5)-f(4.5) = 1 = f(1.5)-f(0.5)#
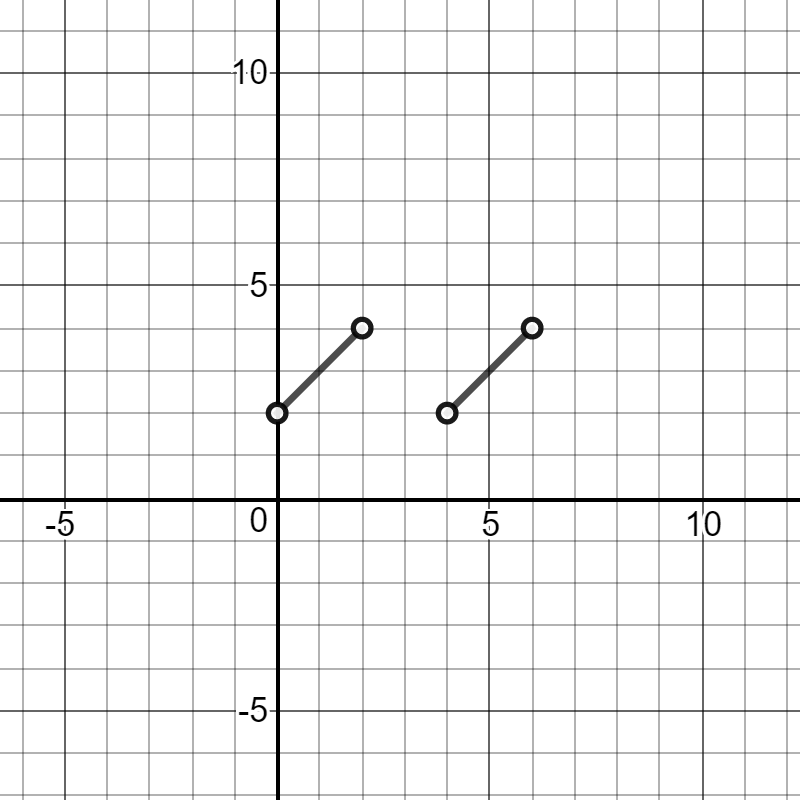
The function
#f(x) = {(x+2,"if",0 < x < 2),(x-2,"if",4 < x < 6):}# satisfies the given condition but fails A, B, and C. The graph is shown below.