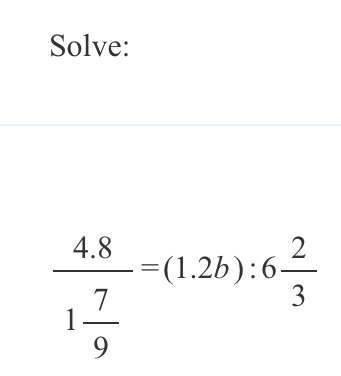The term #(1.2b):6 2/3# can be rewritten as: #(1.2b)/(6 2/3)#
So the question is asking to solve the following equation for #b#:
#4.8/(1 7/9) = (1.2b)/(6 2/3)#
Change the mixed fractions to improper fraction
#1 7/9 = 1 + 7/9 = (9/9 xx 1) + 7/9 = 9/9 + 7/9 = (7 + 9)/9 = 16/9#
#6 2/3 = 6 + 2/3 = (3/3 xx 6) + 2/3 = 18/3 + 2/3 = (18 + 2)/3 = 20/3#
We can now rewrite the problem as:
#4.8/(16/9) = (1.2b)/(20/3)#
Or
#(4.8/1)/(16/9) = ((1.2b)/1)/(20/3)#
We can use this rule for dividing fractions to rewrite each side of the equation:
#(color(red)(a)/color(blue)(b))/(color(green)(c)/color(purple)(d)) = (color(red)(a) xx color(purple)(d))/(color(blue)(b) xx color(green)(c))#
#(color(red)(4.8)/color(blue)(1))/(color(green)(16)/color(purple)(9)) = (color(red)(1.2b)/color(blue)(1))/(color(green)(20)/color(purple)(3))#
#(color(red)(4.8) xx color(purple)(9))/(color(blue)(1) xx color(green)(16)) = (color(red)(1.2b) xx color(purple)(3))/(color(blue)(1) xx color(green)(20))#
#43.2/16 = (3.6b)/20#
Next, multiply each side of the equation by #color(red)(20)/color(blue)(3.6)# to solve for #b# while keeping the equation balanced:
#color(red)(20)/color(blue)(3.6) xx 43.2/16 = color(red)(20)/color(blue)(3.6) xx (3.6b)/20#
#864/57.6 = cancel(color(red)(20))/cancel(color(blue)(3.6)) xx (color(blue)(cancel(color(black)(3.6)))b)/color(red)(cancel(color(black)(20)))#
#15 = b#
#b = 15#