Please help show that #((delT)/(delP))_S = (ValphaT)/C_P#?
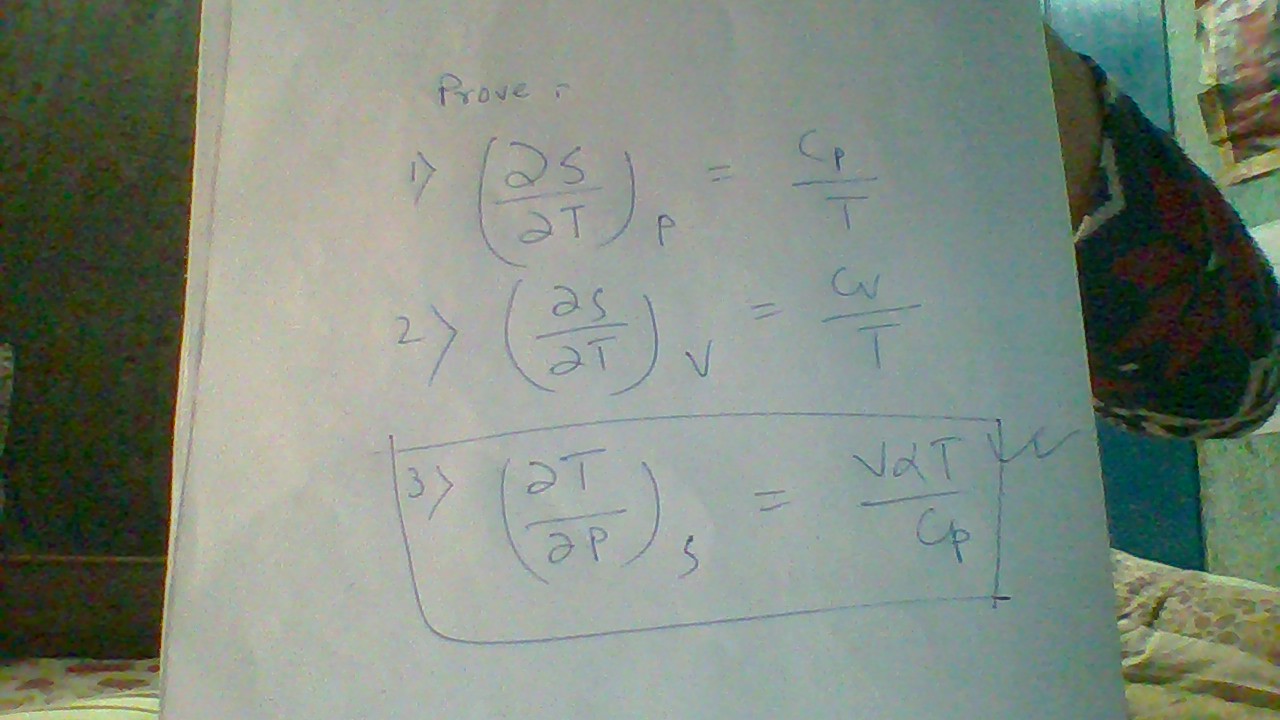
1 Answer
Okay, considering that
#dS = ((delS)/(delT))_PdT + ((delS)/(delP))_TdP# #" "" "bb((1))#
Now, if we divide by
#cancel(((delS)/(delP))_S)^(0) = ((delS)/(delT))_P((delT)/(delP))_S + ((delS)/(delP))_Tcancel(((delP)/(delP))_S)^(1)#
since a constant
#S# forces a derivative of#S# with respect to any variable to go to#0# , and#(dP)/(dP) = 1# no matter what else is held constant.
From this question, we can refer back and recall that
#((delS)/(delT))_P = 1/T ((delH)/(delP))_T = C_P/T# .
#bb((3))#
Now we need to figure out what
The bottom of the derivative shows
#dG = -SdT + VdP# ,
we can either recall the cyclic relation
#dG = ((delG)/(delT))_PdT + ((delG)/(delP))_TdP# ,
showing that
#((del^2G)/(delPdelT))_(P,T) = ((del^2G)/(delTdelP))_(T,P)# ,
meaning that
#-((delS)/(delP))_T = ((delV)/(delT))_P# .#" "" "bb((4))#
Therefore, from
#((delV)/(delT))_P = C_P/T((delT)/(delP))_S#
#=> ((delT)/(delP))_S = T/C_P ((delV)/(delT))_P#
Finally, recall that
#=> color(blue)(((delT)/(delP))_S = (ValphaT)/C_P)#

