Please help with this physics problem?
A small ball of mass M is connected to a block of mass 2M by a light extensible string of length R.The block and the ball are kept on the round.There is sufficient friction to prevent the block from slipping.The ball is projected vertically up with a velocity U.The velocity U for which the centre of mass of the block and the ball moves in a circle satisfies the equation:
#(a)3gr<=U^2>=2gr#
#(b)U^2>=5gr#
#(c)2gr<=U^2<=5gr#
#(d)"None " "of" " these"#
please explain the solution in detail.
A small ball of mass M is connected to a block of mass 2M by a light extensible string of length R.The block and the ball are kept on the round.There is sufficient friction to prevent the block from slipping.The ball is projected vertically up with a velocity U.The velocity U for which the centre of mass of the block and the ball moves in a circle satisfies the equation:
please explain the solution in detail.
2 Answers
None of the above.
The correct condition is
Explanation:
I am assuming that the initial configuration was one in which the string is stretched out straight so that the ball is at distance
I am also assuming that the words "moves in a circle" actually means "moves in a complete semicircle". After all, due to the presence of the ground, it can not describe anything more than a semicircle . On the other hand "complete" is necessary - otherwise no matter what the velocity, the center of mass will, at least initially, describe a part of a circle.
The center of mass will move along a complete semicircle if two conditions are satisfied
- the ball moves along a complete semicircle.
- the block stays fixed on the ground throughout
(under these conditions the center of mass will move all the way along a semicircle of radius#R/3# )
For this, the string must be taut throughout (the tension in the string must at least be zero), and the upward component of the tension can never be more than
If the velocity is
with the vertical, we have :
From conservation of energy :
From Newton's second law (for the component along the string)
The minimum value that
So
On the other hand, the vertical component of the tension at
We need to ensure that the largest value of this component is not more than
It is easy to maximize an expression of the form
so that the maximum value is
So, the largest value of
and so
Thus the condition that one is aiming for is
Note : it may be mistakenly assumed that
and this would have led to
None of these.
Explanation:
Assuming that the initial string elongation is
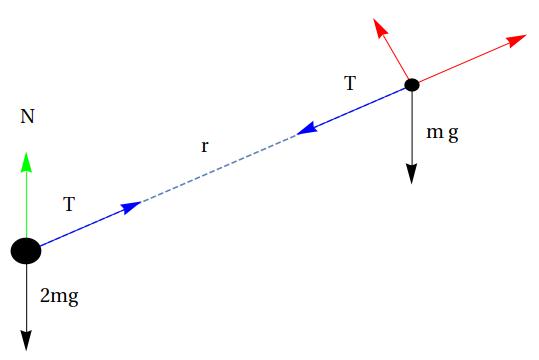
In the attached picture can be depicted the main elements involved. In red
the tension
after substitution
then
then if we choose
Considering the normal reaction in the base body
Here
and then
Considering now that
Resuming, the condition for a neat path is


