Please prove?
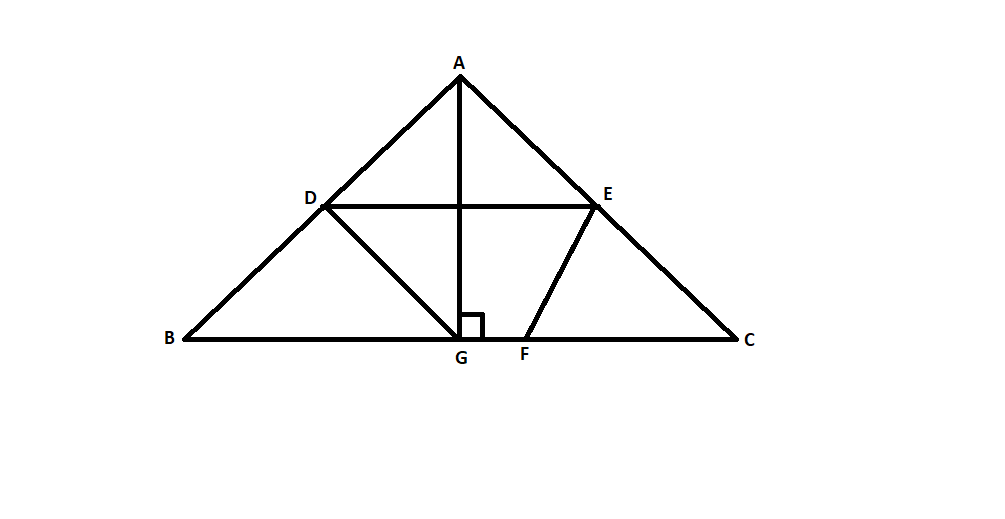
In the figure, D,E and F are the mid points of sides AB, AC and BC respectively and AG is perpendicular on BC. Prove that DEFG is a cyclic quadrilateral.

In the figure, D,E and F are the mid points of sides AB, AC and BC respectively and AG is perpendicular on BC. Prove that DEFG is a cyclic quadrilateral.
1 Answer
Apr 15, 2018
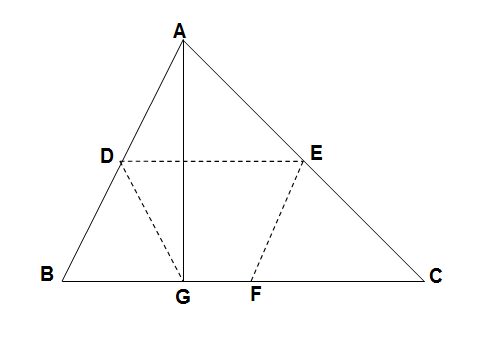
Given:
In
Rtp:
DEFG is a cyclic quadrilateral.
Proof:
As
By midpoints theorem of a triangle we have
Similarly
Now in
So
Hence
So in quadrilateral
This means the quadrilateral

