Question

Please solve q 19?

Answer 1

`DM=3/2` units

Explanation:

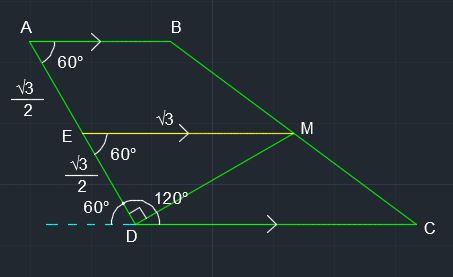
Given `angleDAB=60^@, angleADC=120^@`,
`=> DC` // `AB`
Let `E` be the midpoint of `AD`,
`=> AE=ED=sqrt3/2`
given `M` is the midpoint of `BC, => EM` // `DC` // `AB`
`=> angleDEM=60^@`,
and `EM=(AB+DC)/2=(2*AD)/2=(2sqrt3)/2=sqrt3`
In `DeltaEDM`, as `EM=2ED, and angleDEM=60^@`,
`=> angleEMD=30^@, => angleEDM=90^@`,
`=> DeltaEDM` is right angled at `D`,
`=> DM=EMsin60=sqrt3*sqrt3/2=3/2` units

Or if you are not sure if `DeltaEDM` is a right triangle, you can also use the law of cosines to find the length `DM`,
`DM^2=ED^2+EM^2-2*ED*EM*cos60`,
`=> DM^2=(sqrt3/2)^2+sqrt3^2-2*sqrt3/2*sqrt3*1/2`
`=> DM^2=3/4+3-3/2=9/4`
`=> DM=sqrt(9/4)=3/2` units