Please solve question 149?
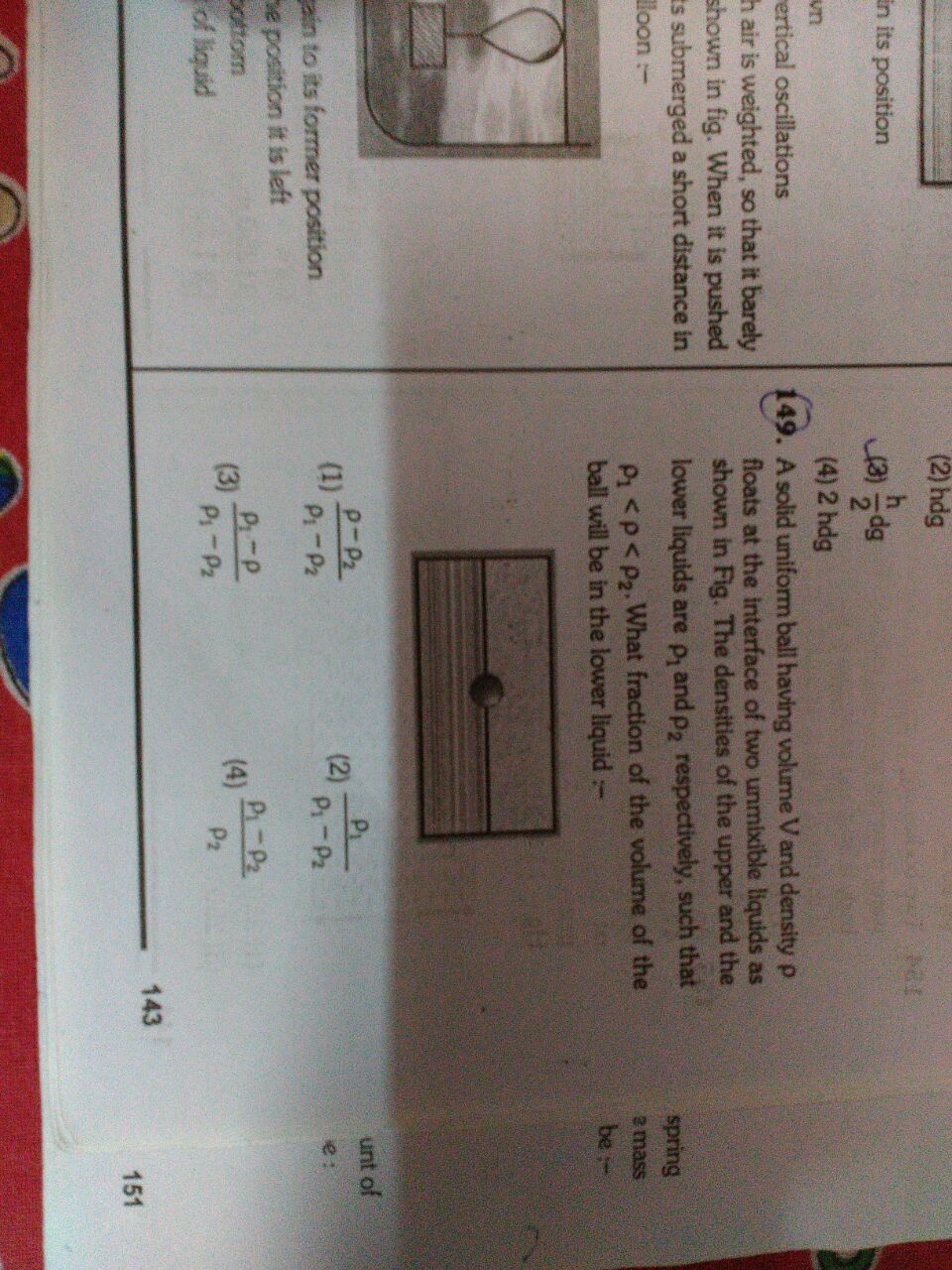
2 Answers
Explanation:
Volume of ball = Volume of liquids displaced
#"V" = "V"_1 + "V"_2 color(white)(...)……(1)#
Weight of ball = Weight of
The answer is
Explanation:
According to Archimedes ' principle
Let the volume of the upper part be
The weight of fluid displaced is
Let the volume of the lower part be
The weight of fluid displaced is
The weight of the ball is
Therefore,
The fraction is
Let,
Therefore,
The answer is


