Evaluate the limit? #lim_(x->0) (e^x-1-x-1/2x^2)/x^3#
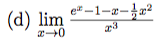
1 Answer
Explanation:
We have that:
So obviously we have an indeterminate form of
if
So taking the derivative of the numerator:
And the derivative of the numerator:
We have ran into an indeterminate form again, so we will apply L'Hôpital's rule a second time and differentiate again:
Again we have ran into an indeterminate form so we need to keep going:
Therefore:
So we finally got there in the end. A quick plot of the graph confirms our results:
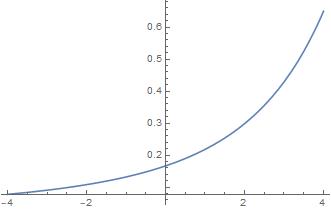
As can be seen the line intersects the axis at 1/6.


