Points A and B are at #(4 ,6 )# and #(7 ,5 )#, respectively. Point A is rotated counterclockwise about the origin by #pi/2 # and dilated about point C by a factor of #1/2 #. If point A is now at point B, what are the coordinates of point C?

Question

1760 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-08T02:25:06

#color(green)("Coordinates of " C = (5,(3/2))#

#A(4,6), B(7,5), "counterclockwise rotation " #pi/2#, "dilation factor" 1/2#

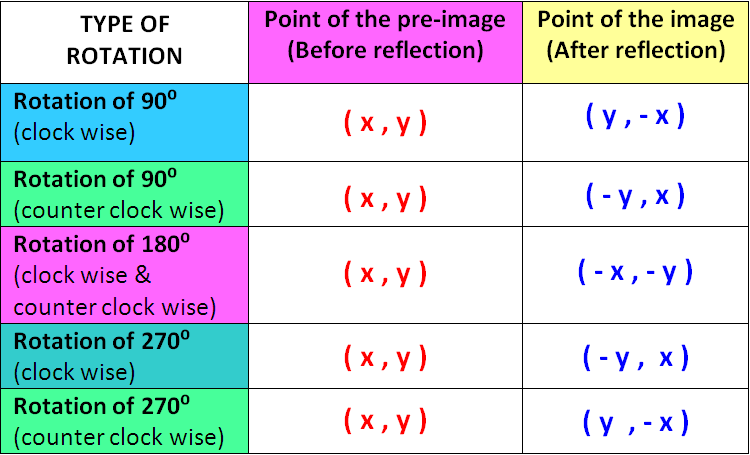
New coordinates of A after #(3pi)/2# counterclockwise rotation

#A(4,6) rarr A' (-6,4)#

#vec (BC) = (1/2) vec(A'C)#

#b - c = (1/2)a' - (1/2)c#

#(1/2)c = -(1/2)a' + b#

#(1/2)C((x),(y)) = -(1/2)((-6),(4)) + ((7),(5)) = ((10),(3))#

#color(green)("Coordinates of " 2 *C ((10),3) = C(5,(3/2))#