Points A and B are at #(9 ,2 )# and #(1 ,5 )#, respectively. Point A is rotated counterclockwise about the origin by #(3pi)/2 # and dilated about point C by a factor of #3 #. If point A is now at point B, what are the coordinates of point C?

Question

1187 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-08T02:19:59

#color(blue)("Coordinates of " C ((7/2),-11)#

#A(9,2), B(1,5), "rotation " #(3pi)/2#, "dilation factor" 3#

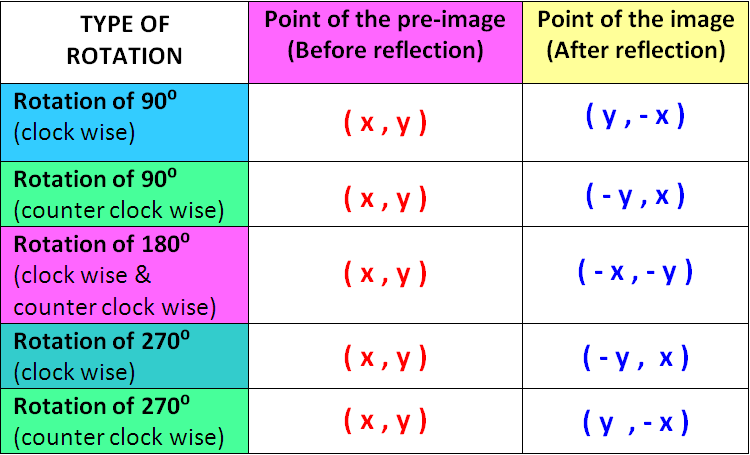
New coordinates of A after #(3pi)/2# counterclockwise rotation

#A(9,2) rarr A' (2,-9)#

#vec (BC) = 3 vec(A'C)#

#b - c = 3a' - 3c#

#2c = 3a' - b#

#2C((x),(y)) = 3((2),(-9)) + ((1),(5)) = ((7),(-22))#

#color(blue)("Coordinates of " (1/2)C ((7),-22) = C ((7/2),-11)#