Question

Proof of the fundamental theorem of calculus?

dA/dx=limΔx→A(x+Δx)-A(x)/Δx
The difference quotient represents the area between x and x+Δx. How is this area exactly equal to the area of the rectangle with base delta x and whose height is f(x) where x is a chosen point between x and x+Δx?

dA/dx=f(x) then using leibniz notation we can integrate dA=f(x)dx A(x) is one of the anti derivatives of f(x) but if F(x) is any antiderivative of f(x) then F(x) and A(x) must differ by a constant by the Mean value theorm.
So does F(x) also represent the area below the curve y=f(x) but is stretched by c units?
If F(x) does represent the area below the curve then F(a) must equal zero because the rectangle is infinitely thin (integral from a to a of f(x)=0.

I can't draw the connection between A(x) and F(x) geometrically

Answer 1

Let's look at a particular example.

Explanation:

Let `f(x) = 2x+3` and `I = [1,5]`.

Here is the graph:

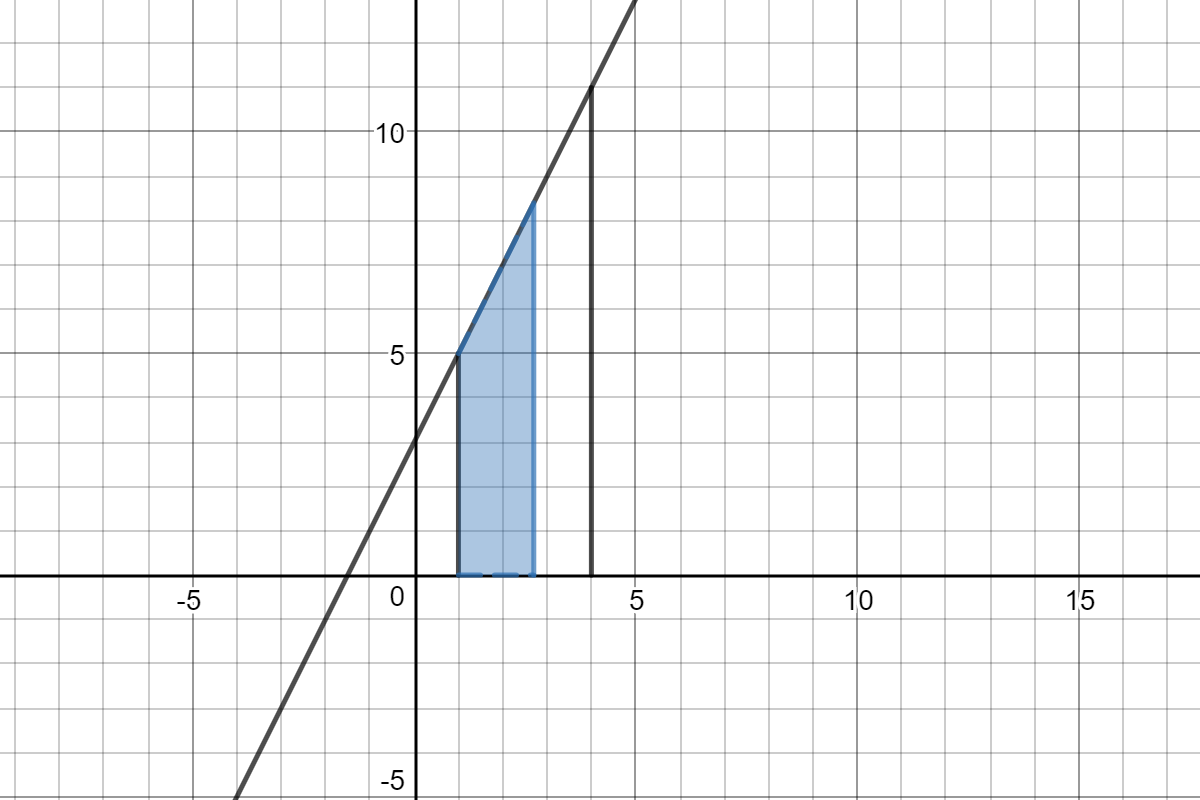
For every `x` in `I`, define `F(x)` by

`F(x) = int_1^x f(t) dt`

In the picture the blue region show the area under the graph from `1` to `x`. (I have used `x = 2.7` for the example.)

This area is `F(x)`. (Note that there is no additional constant.

In fact, we can use geometry to find the area of this triangle atop a rectangle or use what you are apparently calling the First Fundamental Theorem. (I am used to numbering and proving them them the other way around.)

`F(x) = int_1^x f(t) dt`

`= int_1^x (2t+3) dt`

`= [t^2+3t]_1^x`

`= x^2+3x-4`

So, `F(x) = x^2+3x-4` is the area under the graph from `1` to `x`.

I believe that this is also what you are calling `A(x)`.

They are identical.

We could have chosen a different antiderivative to find `F(x)`

For example:

`F(x) = int_1^x f(t) dt`

`= int_1^x (2t+3) dt`

`= [t^2+3t+7]_1^x`

`= (x^2+3x+7)-(1^2-3(1)+7)`

`= x^2+3x-4`

We get the same `F(x)` because `F(x)` is fully determined by `f` and `a=1`.
.
The `F(x)` defined in (2) is not a general antiderivative. It is a particular antiderivative. It must satisfy `F(a) = 0`.
In such a case, there is no constant of integration.

Answer 2

We seek the proof of the FTC, ie:

`d/dx \ int_a^x \ f(x) \ dx = f(x)`

If we think of the geometric integration of the integral, that is

`A(x) =int_a^x \ f(x) \ dx`

represents the area under a curve, the the theorem tells us that the rate of change of the area function is the same as the function itself

The wikipedia page on the Fundamental theorem of calculus provides an excellent geometric understanding of the theorem, and that page serves as the source for most of this solution.

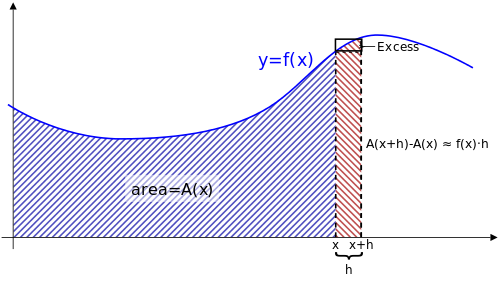
If we consider an Area function, `A(x)` that represents the area under the curve `y=f(x)`, bounded by the `x`-axis, some arbitrary start-point `a` and some variable end-point `x`, as pictured in `color(blue)(blue)`.

Now, consider an additional portion of area, where we have a small strip of width `h`, as pictured in `color(red)(red)` . Using our area function we can define the exact area, using:

`A(x+h)`

Then we can define the portion of `color(red)(red)` area, as:

`A_(red) = A(x+h) - A(x)`

But as `h` is small, we can also approximate that area by treating it as a rectangle, thus

`A_(red) ~~ hf(x) => A(x+h) - A(x) ~~ h f(x)`

Hence we have:

`f(x) ~~ (A(x+h) - A(x))/h`

As we make `h` smaller and smaller, then the error in the approximation (or excess) also becomes smaller and smaller, and the estimate becomes more accurate. Thus in the limit, as `h rarr 0`, we have

`f(x) = lim_(h rarr 0) (A(x+h) - A(x))/h`

This limit should look familiar, as it is the limit definition of the derivative, and so:

`lim_(h rarr 0) (A(x+h) - A(x))/h = A'(x) = f(x)`

Which is what we wanted to show.

Source : Wikipedia