Prove by vector method that #sinA/a=sinB/b=sinC/c#?

Question

28804 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-08-04T20:25:02

Please see below.

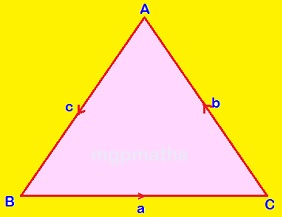
Let , #vec(AB)=bar(c) ,# #vec(BC)=bar(a) ,# #vec(CA)=bar(b) #

. enter image source here #

So,

#bar(a)+bar(b)+bar(c)=bar(0)#

Using definition of cross Product

#bar(a)xx(bar(a)+bar(b)+bar(c))=bar(a)xxbar(0)#

#=>(bar(a)xxbar(a))+(bar(a) xxbar(b))+(bar(a) xxbar(c))=bar(0)to[becausebar(a)xxbar(0)=bar(0) ]#

#=>bar(0)+(bar(a) xxbar(b))+(bar(a) xxbar(c))=bar(0)to[because(bar(a)xxbar(a))=bar(0)]#

#=>(bar(a) xxbar(b))-(bar(c)xxbar(a))=bar(0)#

#=>(bar(a) xxbar(b))=(bar(c)xxbar(a))#

#=>a*bsin(pi-C)=c*asin(pi-B)#

#=>bsinC=csinB#

#=>sinC/c =sinB/b....to(1)#

Similarly we can prove that ,

#=>sinA/a =sinB/b....to(2)#

Hence ,

#sinA/a =sinB/b=sinC/c #