Prove that?
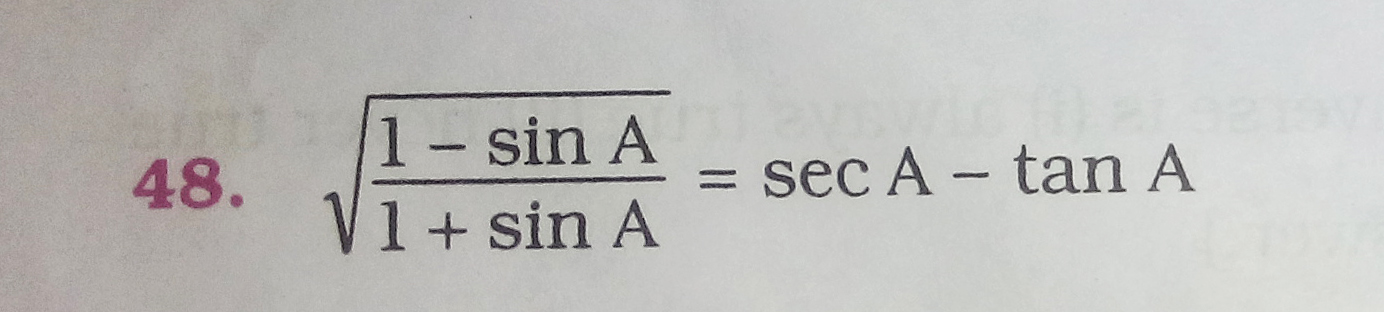
2 Answers
See explanation.
Explanation:
Your first aim should be to get rid of the square root, by making everything within it squared. You'll need to use some identities for this.
Applying
Now the numerator is squared, but the denominator still needs to changed using the identity
The squares can cancel out the square root...
Kindly, refer to a Proof given in the Explanation.
Explanation:
Here is another way to solve the Problem :
We know that,
But,
Thus, we conclude from
Multiplying the corresponding sides, we get,
Enjoy Maths.!

