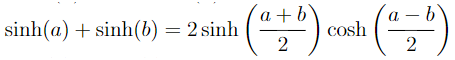You must know the definition of #sinh# and #cosh# to show this.
By definition:
#sinh x = (e^x - e^-x)/2# and
#cosh x = (e^x + e^-x)/2#
So we rewrite the left-hand-side of the equation as follows:
#sinh(a) + sinh(b) = (e^a - e^-a)/2 + (e^b - e^-b)/2#
This becomes:
#= (e^a - e^-a + e^b - e^-b)/2#
and rearranging gives:
#= (e^a - e^-a + e^b - e^-b)/2# (Eq.A)
Now for the right-hand-side of the equation, we have:
#2 sinh((a+b)/2) cosh((a-b)/2)= 2 [(e^((a+b)/2) - e^(-(a+b)/2))/2] [(e^((a-b)/2) + e^(-(a-b)/2))/2]#
We can simplify this by cancelling out the #2# and #1/2# and keep only one #1/2#:
#= 1/2 [e^((a+b)/2) - e^(-(a+b)/2)] [e^((a-b)/2) + e^(-(a-b)/2)]#
we can also factor out #e^(1/2)# as it appears everywhere:
#= e^(1/2)/2 [e^(a+b) - e^(-a-b)] [e^(a-b) + e^(-a+b)]#
which becomes:
#= e^(1/2)/2 [e^(a+b+a-b) + e^(a+b-a+b)-e^(-a-b+a-b) - e^(-a-b -a+b)]#
which simplifies to:
#= e^(1/2)/2 [e^(2a) + e^(2b)-e^(-2b) - e^(-2a)]#
multiply back by #e^(1/2)# and rearrange:
#= 1/2 [e^(a)- e^(-a) + e^(b)-e^(-b) ]#
and you readily see that this is the same as our (Eq.A):
#= (e^(a)- e^(-a))/2 + (e^(b)-e^(-b))/2 = sinh(a) + sinh(b)#
So the left and right parts of the equation are the same and the identity is correct.
Q.E.D.