Prove this ?
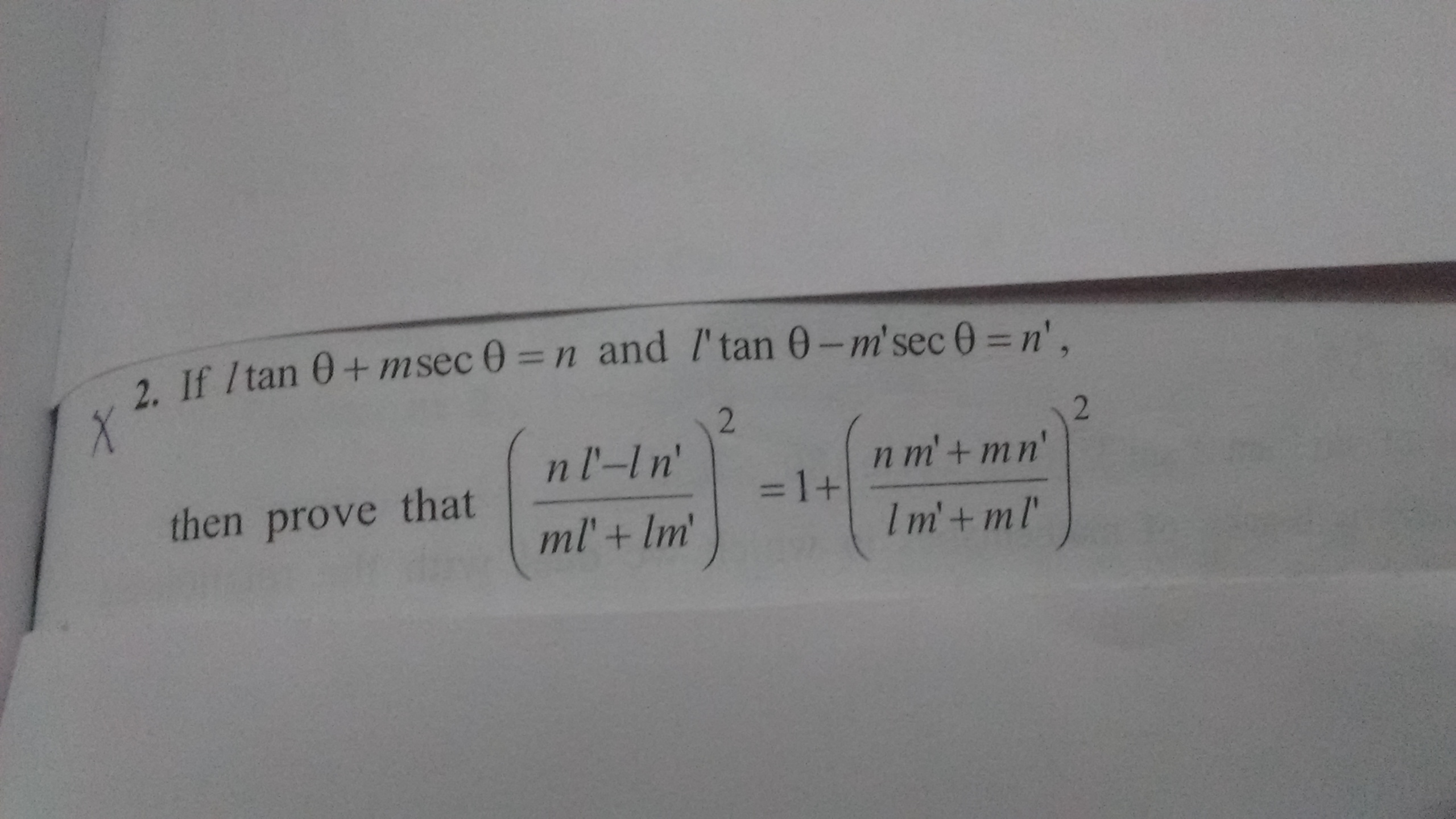
2 Answers
see below
Explanation:
Prove
Please refer to a Proof given in the Explanation Section.
Explanation:
We rewrite these eqns. as,
Using Kramer's Method to solve these eqns. for
Since,
Enjoy Maths.!
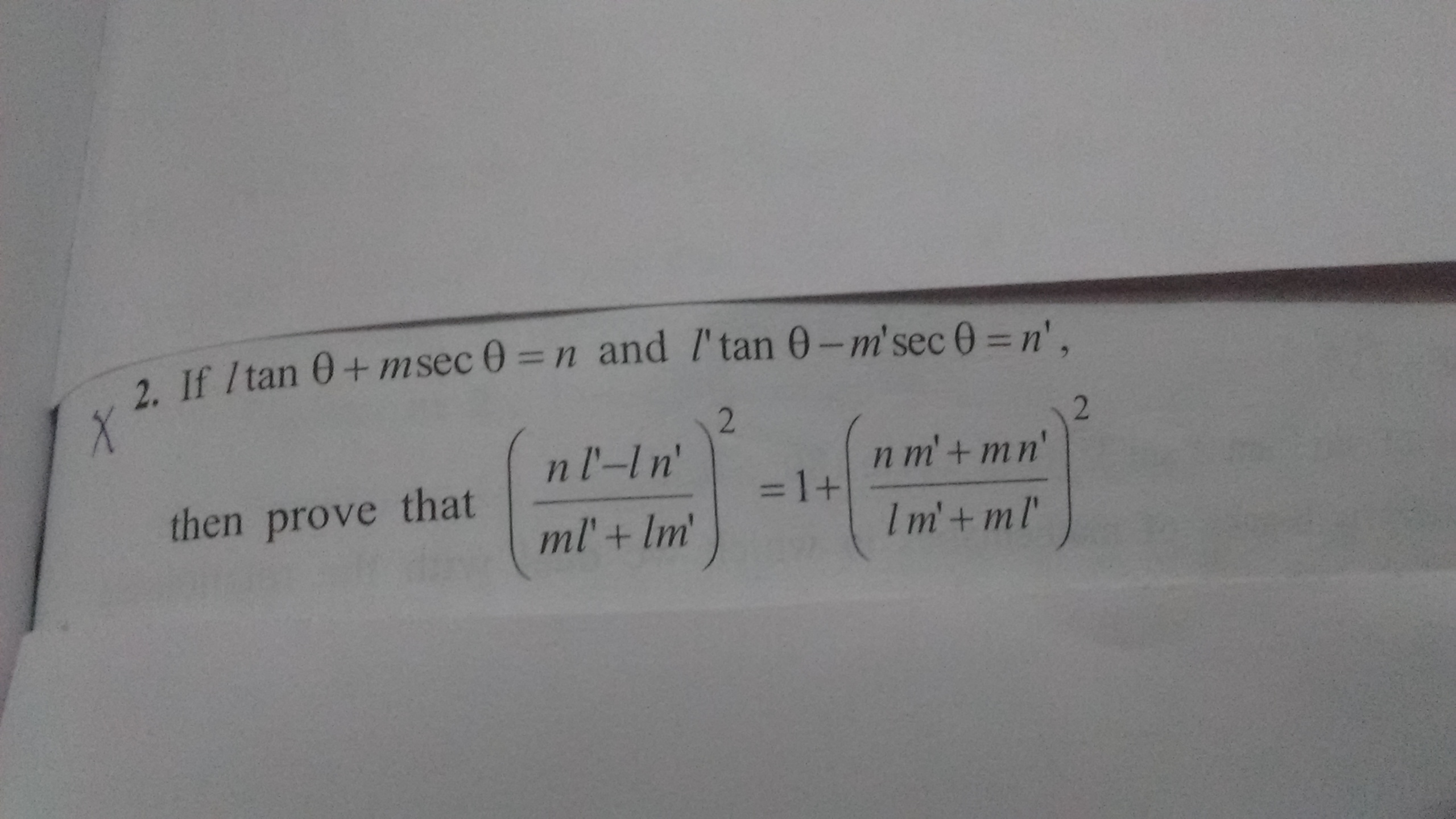
see below
Prove
Please refer to a Proof given in the Explanation Section.
We rewrite these eqns. as,
Using Kramer's Method to solve these eqns. for
Since,
Enjoy Maths.!