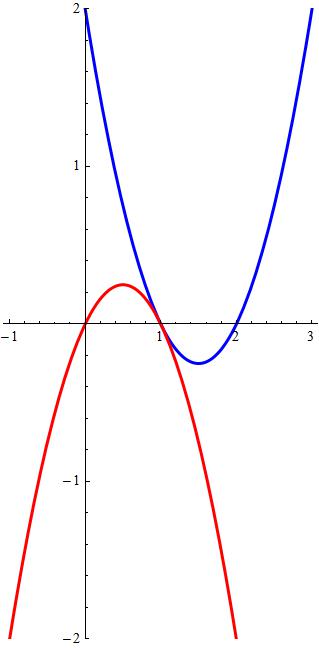
Quadratics having a common tangent #y = x^2 + ax + b# and #y = cx -x^2# have a common tangent line at the point (1,0), how do you find #a, b# and #c#?

Question

13125 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-03T10:04:50

#{a = -3, b = 2, c = 1}#

Calling #f(x) = x^2 + ax + b# and #g(x) = cx -x^2# we have the conditions:

#f(1) = 1 + a + b = 0#
#g(1) = c - 1 = 0#
Now, calling #df(x) = 2x+a# and #dg(x) = c-2x# we have also
#df(1) - dg(1) = 2+a-c+2=0#

Solving for #a,b,c#

#{ ( 1 + a + b = 0), ( c - 1 = 0), (a-c+4=0) :}#

we obtained

#{a = -3, b = 2, c = 1}#

Attached the tangent conics plot.

enter image source here