Question

Quadrilateral JKLM has vertex coordinates J(2,4), K(6,1), L(2,-2), and M(-2,1). What type of quadrilateral is JKLM?

Answer 1

The Quadrilateral JKLM having vertex coordinates at `J(2,4), K(6,1), L(2,-2), and M(-2,1)` is a Rhombus.

Explanation:

`" "`
A quadrilateral satisfies the following properties:

(1) Four sides (also called edges)

(2) Four vertices (also called corners)

(3) Interior angles add to 360 degrees

Types of Quadrilaterals:

(i) Parallelogram

(ii) Rectangle

(iii) Rhombus

(iv) Square

(v) Trapezoid (US) or Trapezium (UK)

(vi) Kite

Construct the quadrilateral JKLM on a Cartesian coordinate plane:

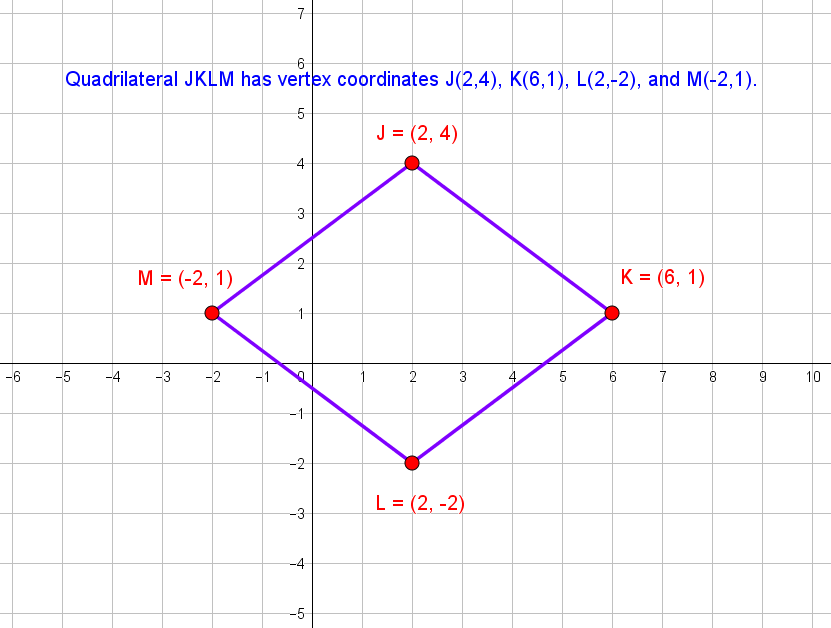
Measure the magnitudes of the line segments `bar (JK), bar(KL), bar(LM) and bar(MJ)`

Also measure the Internal angles at the vertices.

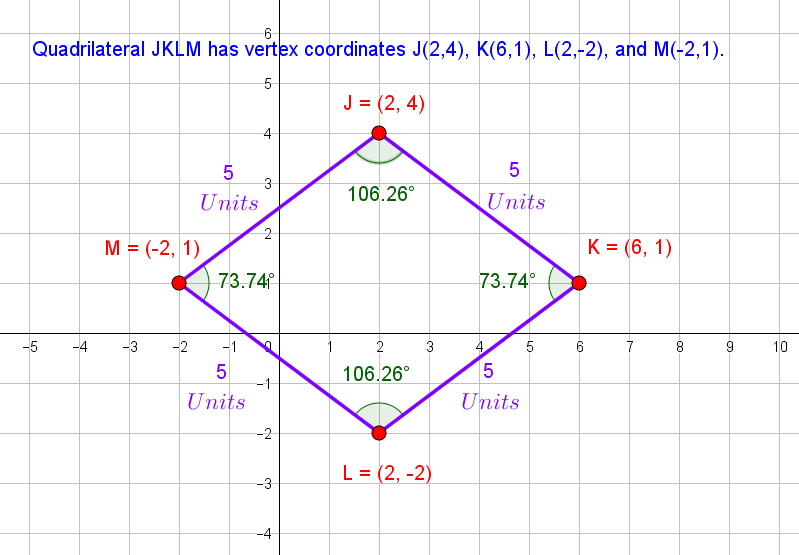
Observe that All the Sides are of equal length in the Quadrilateral JKLM.

So, `bar (JK), bar(KL), bar(LM) and bar(MJ)="5 Units"`.

Opposite angles are congruent.

`/_ JML = /_JKL = 73.74^@` and

`/_MJK = /_MLK = 106.26^@`

In the next step, draw the diagonals and analyze the point of intersection.

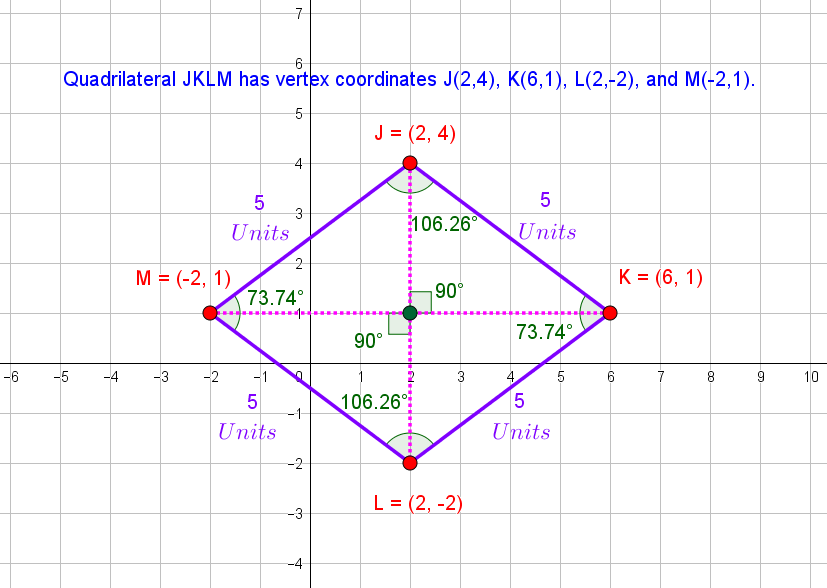
Observe that the diagonals bisect each other at right angles.

You can also verify that the opposite sides are parallel.

Hence, `JM | | KL and JK | | ML`

In a Rhombus, the following properties are true:

(a) Diagonally opposite angles are equal.

(b) All sides are of equal lengths.

(c) Opposite sides are parallel.

(d) The diagonals bisect each other at 90°.

Hence,

the Quadrilateral JKLM having vertex coordinates at `J(2,4), K(6,1), L(2,-2), and M(-2,1)` is a Rhombus.

Hope it helps.