Determine rate law and rate constant for #2"I"^(-)(aq) + "S"_2"O"_8^(2-)(aq) -> "I"_2(aq) + 2"SO"_4^(2-)(aq)#?
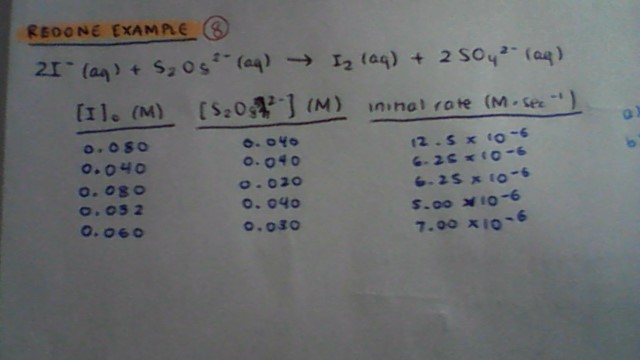
a. determine rate law
b. calculate rate constant
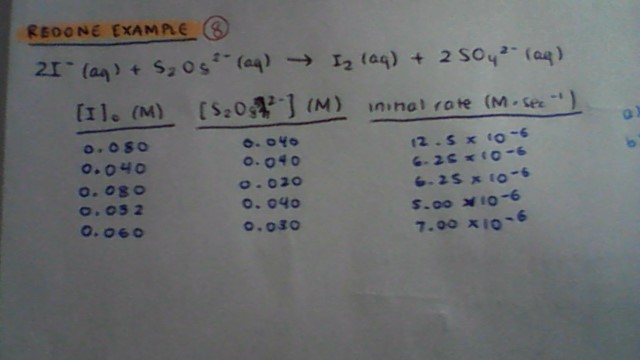
a. determine rate law
b. calculate rate constant
1 Answer
You've given:
#2"I"^(-)(aq) + "S"_2"O"_8^(2-)(aq) -> "I"_2(aq) + 2"SO"_4^(2-)(aq)#
#ul("trial"" "["I"^(-)]_0("M")" "" "["S"_2"O"_8^(2-)]_0("M")" "" ""init rate"("M/s"))#
#1" "" "0.080" "" "" "" "0.040" "" "" "" "" "12.5 xx 10^(-6)#
#2" "" "0.040" "" "" "" "0.040" "" "" "" "" "6.25 xx 10^(-6)#
#3" "" "0.080" "" "" "" "0.020" "" "" "" "" "6.25 xx 10^(-6)#
#4" "" "0.032" "" "" "" "0.040" "" "" "" "" "5.00 xx 10^(-6)#
#5" "" "0.060" "" "" "" "0.030" "" "" "" "" "7.00 xx 10^(-6)#
Alright, so we know that we can pick two trials where one reactant concentration stayed constant, so that we can take the ratio of the remaining reactant concentration and compare it to the ratio of the rates.
In other words, we take the selective ratio of the rate laws:
#(r_b(t))/(r_a(t)) = (k["I"^(-)]_b^m["S"_2"O"_8^(2-)]_b^n)/(k["I"^(-)]_a^m["S"_2"O"_8^(2-)]_a^n)# where
#a# and#b# represent chosen trials with initial rates#r_k(t)# , and#m# and#n# are to-be-determined exponents (orders) for each reactant in the rate law.#k# is a rate constant that should not change with trials.From here on out, subscripts indicate trial number, and it is implied that we are examining initial concentrations only.
In this case, we can only choose trials
#bb3# over#bb1# for#"I"^(-)# (iodide) to stay constant and#"S"_2"O"_8^(2-)# (dithionate) to change.We'll write it the full way first, and the shortcut way second:
#(r_3(t))/(r_1(t)) = (cancelk["I"^(-)]_3^m["S"_2"O"_8^(2-)]_3^n)/(cancelk["I"^(-)]_1^m["S"_2"O"_8^(2-)]_1^n)#
#(6.25)/(12.5) = cancel((0.080)^m/(0.080)^m)^(1)(0.020)^n/(0.040)^n#
#0.50 = 0.50^n# Therefore,
#n = 1# , so the reaction is 1st order with respect to dithionate only.Now we'll do it the shortcut way. We can choose trials that keep dithionate constant, and change iodide. That's a bit harder, but I would choose to divide
#bb2# over#bb1# (although#4# over#1# or#4# over#2# are also valid choices, those numbers aren't as nice).
#(6.25)/(12.5) = (0.040)^m/(0.080)^m#
#0.50 = 0.50^m# So,
#m = 1# as well, and the reaction is also 1st order with respect to iodide only.Therefore, the rate law is:
#color(blue)(r(t)) = k[A]^m[B]^n = color(blue)(k["I"^(-)]["S"_2"O"_8^(2-)])#
Now, the rate constant can be calculated since we know the exponents. Choose any trial. I choose trial 1.
#12.5 xx 10^(-6) "M/s" = k("0.080 M")^1("0.040 M")^1#
#color(blue)(k) = (12.5 xx 10^(-6) "M/s")/(("0.080 M")^1("0.040 M")^1)#
#= color(blue)(3.91 xx 10^(-3) "M"^(-1)cdot"s"^(-1))# or
#1/("M"cdot"s")# , or#"L"/("mol"cdot"s")# .

