Question

Really need help on this question ASAP! Thanks?!

Answer 1

`2 sqrt 3` km from the road on the perpendicular bisector of the line joining the two farms

Explanation:

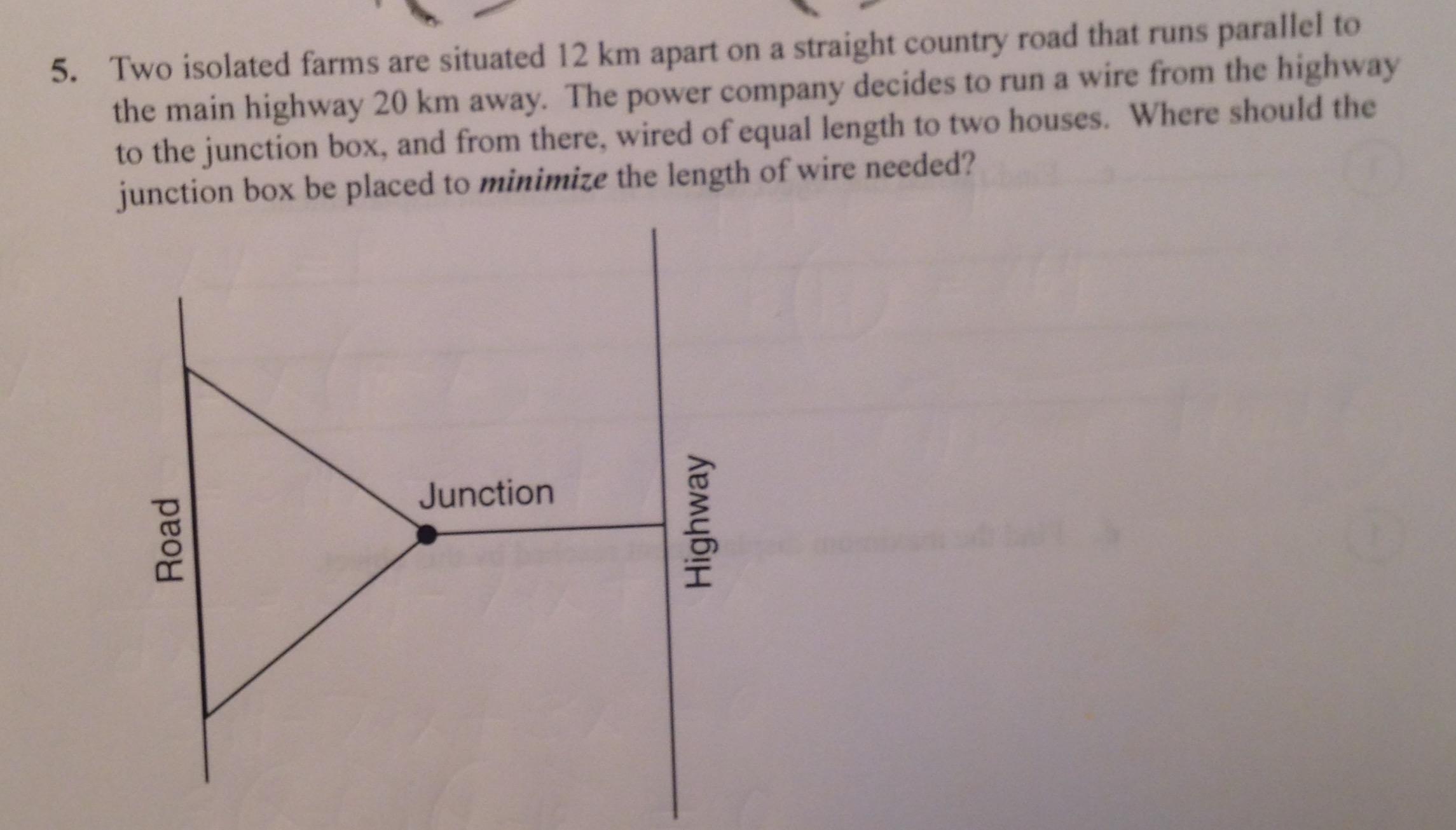
It will help to set up a coordinate system with the origin at the midpoint of the two farms, with the road as the `y` axis. Then the coordinates of the two farms are `(0,a)` and `(0,-a)`, respectively where `a = 6` km. From symmetry, it is easy to see that the junction must be placed on the perpendicular bisector of the line joining the two farms (which is our `x` axis). Let the coordinates of the junction be `(x,0)` and denote the distance between the road and the highway by `D` (`D` is, of course, 12 km).

In this setup, the length of wiring turns out to be
`L = D-x+2 sqrt{x^2 +y^2}`

To minimize this, we differentiate `L` with trespect to `x` and set it equal to zero. Now,

`{dL}/{dx} = -1+{2 x}/sqrt{x^2+y^2}`

and setting this to zero gives you

`{2 x}/sqrt{x^2+y^2}=1`

which implies

`4x^2 = x^2+a^2`

and thus

`x = a/sqrt{3}`

(The negative root of this equation is obviously extraneous, and can be ignored).

Note
If you feel that appealing to symmetry to decide that the junction must be placed on the perpendicular bisector is a bit of a cop-out, here's a geometric argument. If you consider all possible positions of the junction for whom the sum of the lengths of wires from the farms is a constant, then these points will lie on an ellipse. The point on the ellipse that is closest to the highway must lie on the minor axis of this ellipse - which is the perpendicular bisector.

Answer 2

16.5 km from the highway.

Explanation:

If you set up the diagram to show the two legs (y) as the hypotenuse of a triangle, then the junction box divides the main line into two segments, x and 20 – x, which is one side of each triangle. The hypotenuse is:

`y^2 = 6^2 + (20 – x)^2` ; `y^2 = 36 +400 + x^2 – 40x`
`y^2 = x^2 – 40x + 436`
The local minimum of that function is where the first derivative is equal to zero.
`y = 2x – 40`

The minimum total distance must include the line from the highway:

`D = x + 2xx(2x – 40)`; `D = x + 4x – 80` ; `D = 5x – 80` ; `x = 16`

This approximation may be refined by careful differentiation of the whole line, but will serve as a check point for verification.

CHECK:
at x = 14, D = 14 + 816.97 = 30.97
at x = 15, D = 15 + 15.62 = 30.62
at x = 16, D = 16 + 14.422 = 30.422
at x = 16.25, D = 16.25 + 14.15 = 30.40
at x = 16.5, D = 16.5 + 13.89 = 30.39
at x = 16.75, D = 16.75 + 13.65 = 30.397
at x = 17, D = 17 + 13.416 = 30.416
at x = 17.5, D = 17.5 + 13.0 = 30.50
at x = 18, D = 18 + 12.65 = 30.65