Question

Related rates-Weight on rope word problem?

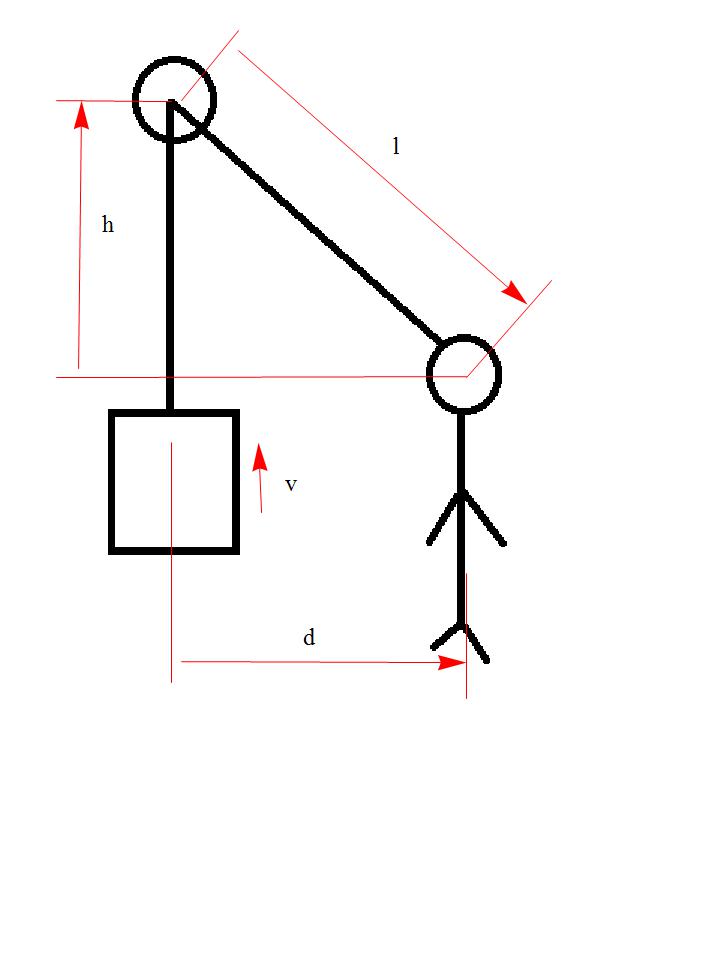
A person walks away from a pulley pulling a rope slung over it. The rope is being held at a height 10 ft below the pulley. Suppose that the weight at the opposite end of the rope is rising at 4 ft/sec

At what rate is the person walking when she/he is 20 ft from being directly under the pulley?

Here is what I did: y represents the distance from one end of the rope whose attached to the weight and the pulley. Given y=10y=10, we can use the Pythagorean theorem to describe the relationship between the three sides of the right angle triangle as 10^2+x^2=z^2. The rate of change of y with respect to time is 4 ft/sec which is also equal to the rate of change of z because the two pieces of the rope are moving with the same speed as the weight moving upwards. The three variables z, x, and y will all change with respect to time as the person gets to pull the rope in the x direction. z′=4 ft/sec y′=4 ft/ sec When x=20, x^2+y^2=z^2. By taking the derivative of both sides of the equation we get 2yy′+2xx′=2zz′, so yy′+xx′=zz

How can I find What the values of z and y are when x=20x=20?

~~~~~~~~~~~~~~~~~~~~~~~

What I am trying to say is, as the person pulls the rope and moves in the x direction the distance of the weight to the pulley is decreasing I am not saying that the length of rope is increasing

Answer 1

See below.

Explanation:

Calling

`d =` horizontal distance under the pulley [20 ft]
`h =` pulley's height (regarding the person's head) [10 ft]
`l =` diagonal from pulley to person's head
`v =` rope rising velocity [4 ft/sec]

we have

`l^2=d^2+h^2` and also deriving regarding time

`2l (delta l)/(delta t)=2d (deltad)/(delta t)+0` because `h = C^(te)`

but assuming the rope inextensible `(delta l)/(delta t) = v =4` ft/sec]

then

`(delta d)/(delta t) =( l/d)v = (sqrt(d^2+h^2)/d)v = (sqrt(1+(h/d)^2))v =2 sqrt5` [ft/sec]

Attached figure explaining the variables used.