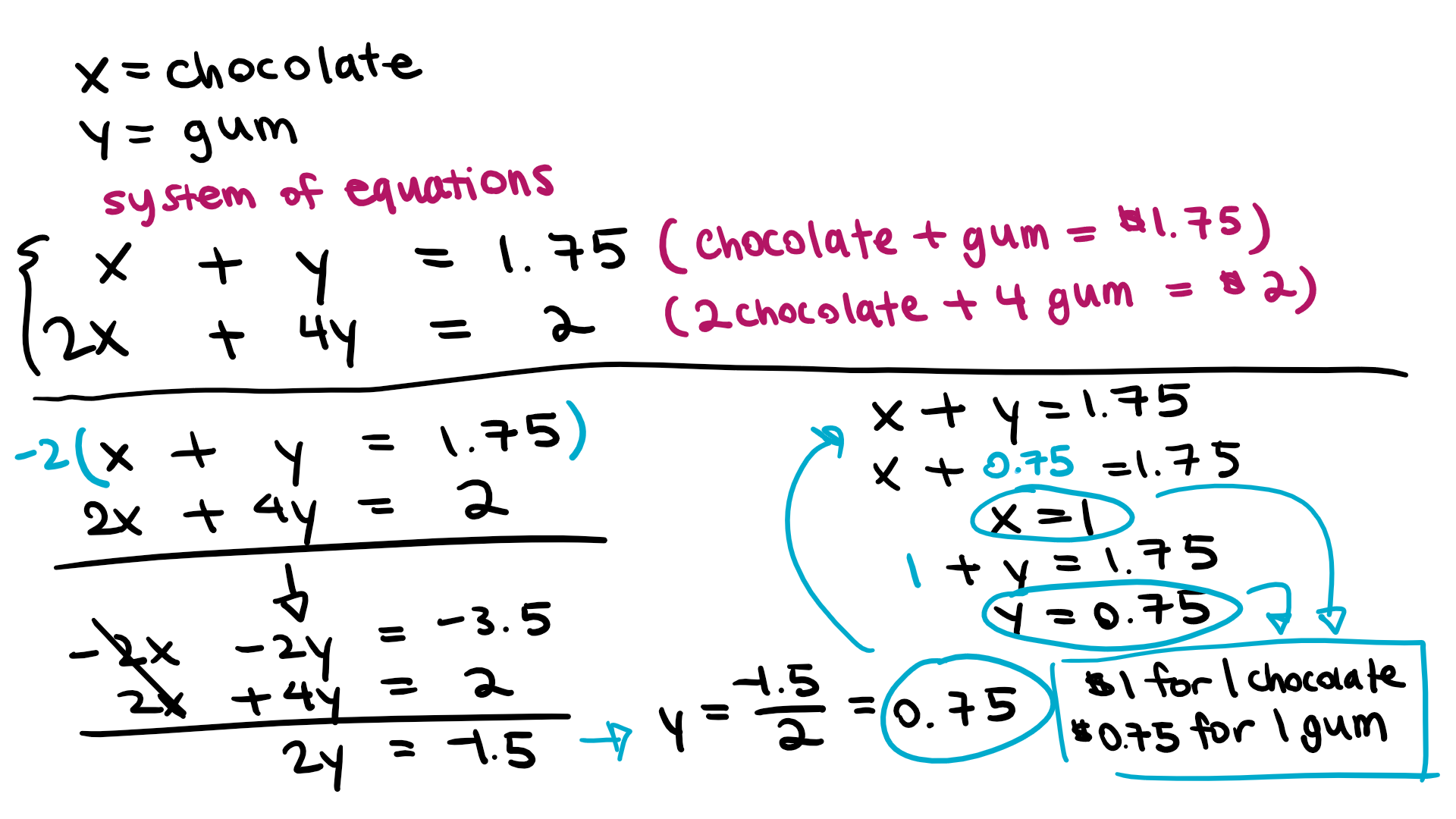Sally bought three chocolate bars and a pack of gum and paid $1.75. Jake bought two chocolate bars and four packs of gum and paid $2.00. Write a system of equations. Solve the system to find the cost of a chocolate bar and the cost of a pack of gum?
2 Answers
Cost of a chocolate bar: $0.50
Cost of a pack of gum: $0.25
Explanation:
Write 2 systems of equations. use
3 chocolate bars and a pack of gum cost $1.75.
Two chocolate bars and four packs of gum cost $2.00
Using one of the equations, solve for y in terms of x.
Now we know the value of y, plug it into the other equation.
Distribute and combine like terms.
Subtract 7 from both sides
Divide both sides by -10.
The cost of a chocolate bar is
Now we know the price of a chocolate bar, plug it back into the first equation.
The cost of a pack of gum is
$1 for 1 chocolate
$0.75 for 1 gum
Explanation:
The set up for the system equations is this:
where
To solve the system of equations, we need to solve for the system of equations for the value of one of the variables. To do that, we must manipulate both equations so that one of the variables can be eliminated (in the image below, I chose to eliminate
After we have one variable (in the image we found the