Question

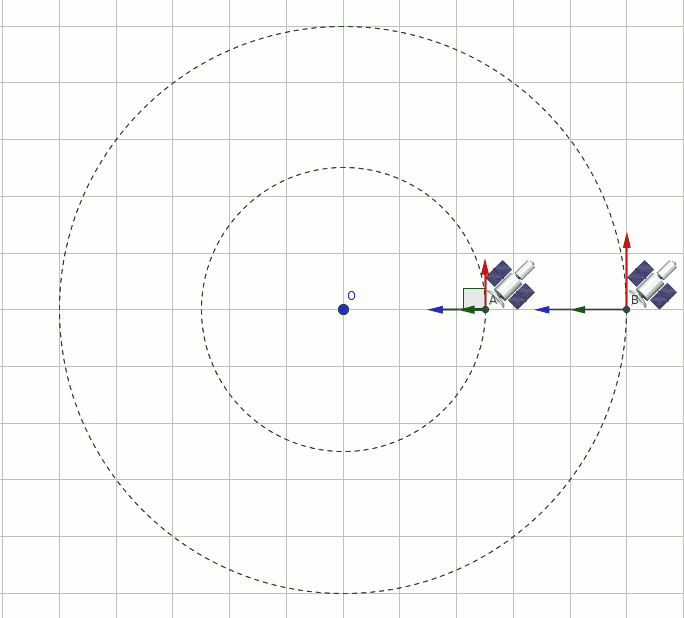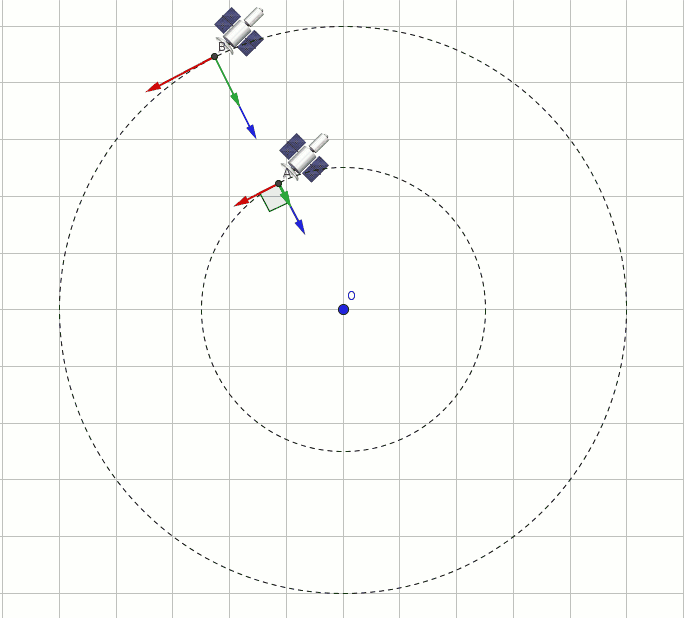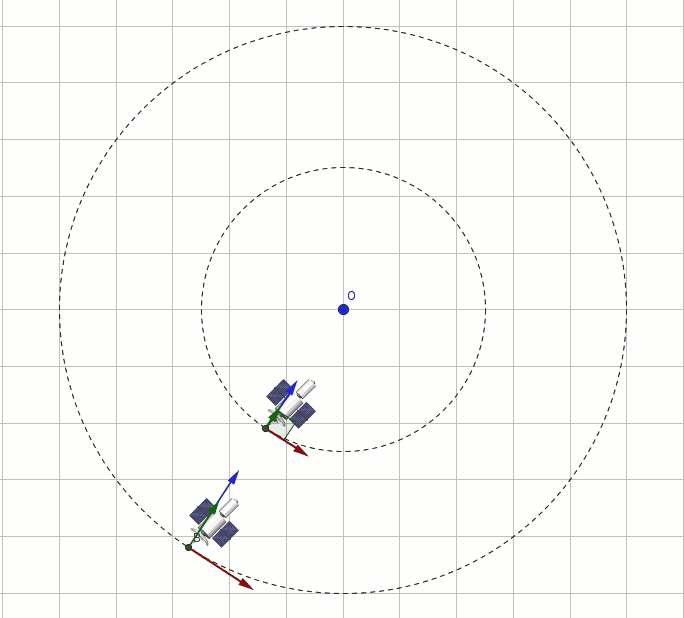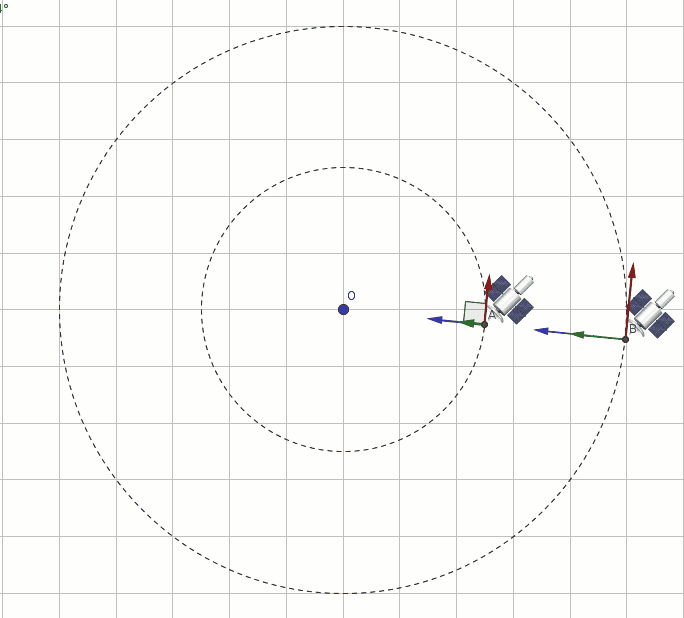
Satellite A orbits a planet with a speed of 10,000 m/s. Satellite B is twice as massive as satellite A and orbits at twice the distance from the center of the planet. What is the speed of satellite B, assuming that both orbits are circular?

Answer 1

`v_B=10000sqrt2 " "m/s`

Explanation:

`"given:"`

`O A=r" ; "OB=2r`

`m_A=m" ; "m_B=2m`

`v_A=10000" "m/s" ; "v_B=?`

`m_P:"mass of planet"`

`(m_A*g_A)/(m_B*g_B)=(K*(m_A*m_P)/r^2)/(K*(m_B*m_P)/(4r^2))`

`"yields"`

`(g_A)/(g_B)=4*(m_A)/(m_B)" (1)"`

`(m_A*g_A)/(m_B*g_B)=((m_A*v_A^2)/r^2)/((m_B*v_B^2)/(4r^2))`

`"yields "`

`(g_A)/(g_B)=4*(v_A^2)/(v_B^2)" (2)"`

`"so "(1)=(2)`

`m_A/(m_B)=v_A^2/(v_B^2)`

`m_A=m" ; "m_B=2m" ;`

`m/(2m)=(v_A^2)/(v_B^2)" ; "v_B^2=2*v_A^2" ; "v_B=v_A*sqrt2`

`v_A=10000" "m/s`

`v_B=10000sqrt2 " "m/s`