Sec theta = 2 to rectangular coordinates??
1 Answer
Feb 26, 2018
See below.
Explanation:
Identity.
For:
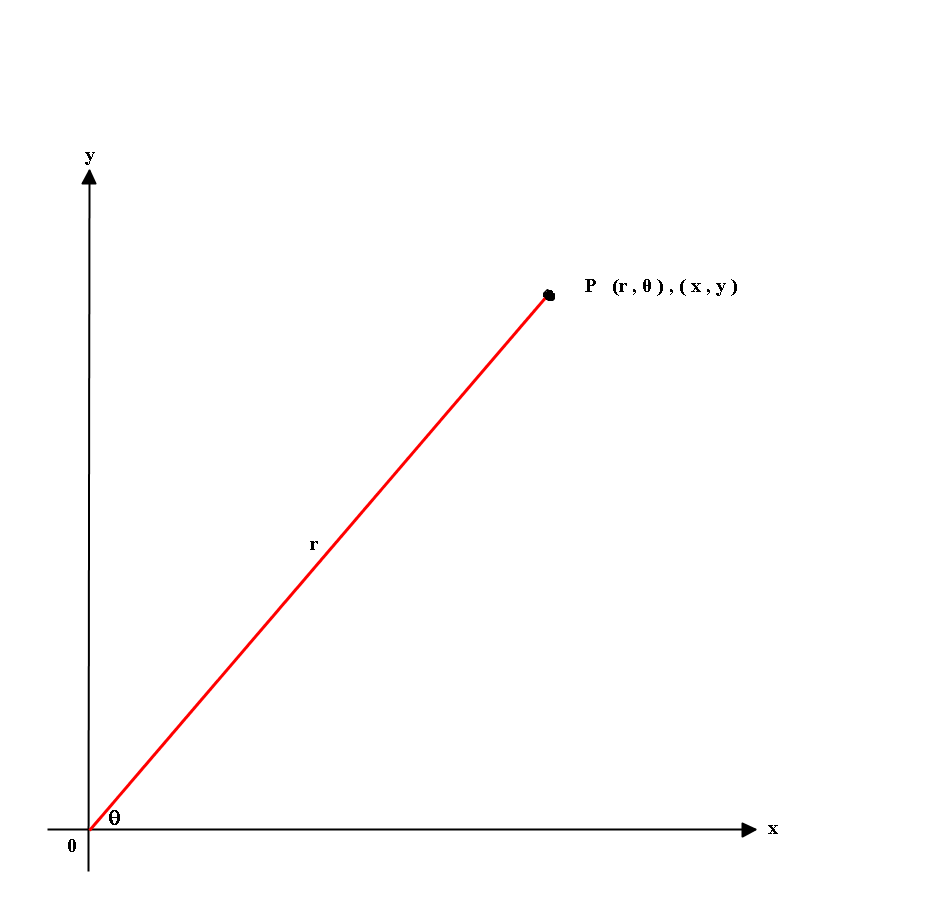
From the above diagram, we can see that:
So coordinates will be:
Without knowing the radius we can't go any further than this.
If this is on a unit circle then the radius is
Coordinates:

