Show that the circles #x^2+y^2+6(x-y)+9=0# touches the co-ordinate axes. Also find the equation of the circle which passes through the common point of intersection of the above circle and the straight line x-y+4=0 and which also passes through the origin?

1 Answer
P dilip_k
Mar 21, 2018

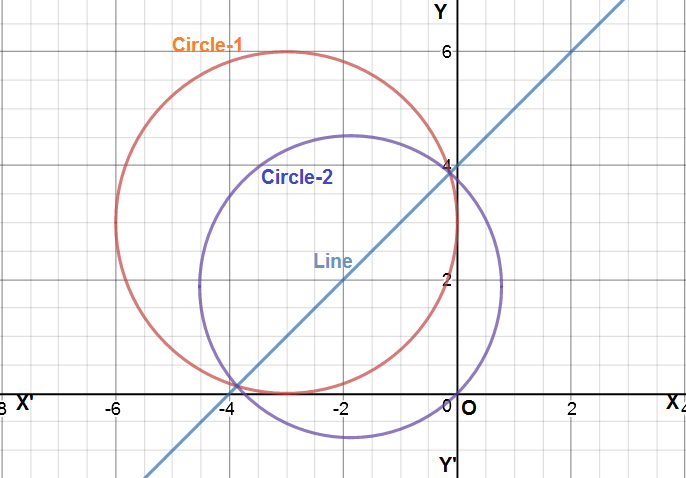
enter image source here

Given equations are

#"Circle"_1->x^2+y^2+6(x-y)+9=0#
and

#"Line"->x-y+4=0#

Now the equation of the given circle

#x^2+y^2+6(x-y)+9=0#

Its standard form becomes

#=>(x+3)^2+(y-3)^2=3^2#

Hence it has center #->(-3,3)# and radius #->3#

As the magnitudes of x- coordinate as well as y-coordinate of the center are same as the magnitude of radius of the circle , the circle's center is equidistant from the coordinate axes . So circles should touch the coordinate axes at (-3,0) and (0,3).

The equation of the set of circle passing through the point of intersection of the #"Circle"_1# and #"Line"# is given by

#"Circle"_1+lambda"line"=0#

#=>x^2+y^2+6(x-y)+9+lambda(x-y+4)=0.........[1]#

By the given condition [1' also passes through origin #(0,0)#

So we can write

#=>0^2+0^2+6(0-0)+9+lambda(0-0+4)=0#

#=> lambda =-9/4#

Inserting the value of lambda in [1] we get the equaiion of the required circle as follows

#x^2+y^2+6(x-y)+9-9/4(x-y+4)=0#

#=>x^2+y^2+6x-6y+9-9/4x+9/4y-9=0#

#=>4x^2+4y^2+24x-24y-9x+9y=0#

#=>4x^2+4y^2+15x-15y=0# #" Circle"_2#

Related questions
Impact of this question
2454 views around the world
You can reuse this answer
Creative Commons License