Show that the path traced by the point of intersection of three mutual perpendicular tangent planes to the ellipsoid #ax^2+by^2+cz^2=1# is a sphere with the same centre as that of the ellipsoid.?
Show that the path traced by the point of intersection of three mutual perpendicular tangent planes to the ellipsoid #ax^2+by^2+cz^2=1# is a sphere with the same centre as that of the ellipsoid.
Show that the path traced by the point of intersection of three mutual perpendicular tangent planes to the ellipsoid
1 Answer
See below.
Explanation:
Calling
If
Let
but
Now given three orthogonal planes
and calling
and as a consequence
then we have also
Now adding
and finally
but
so
which is the path traced by the point of intersection of three mutual perpendicular tangent planes to the ellipsoid.
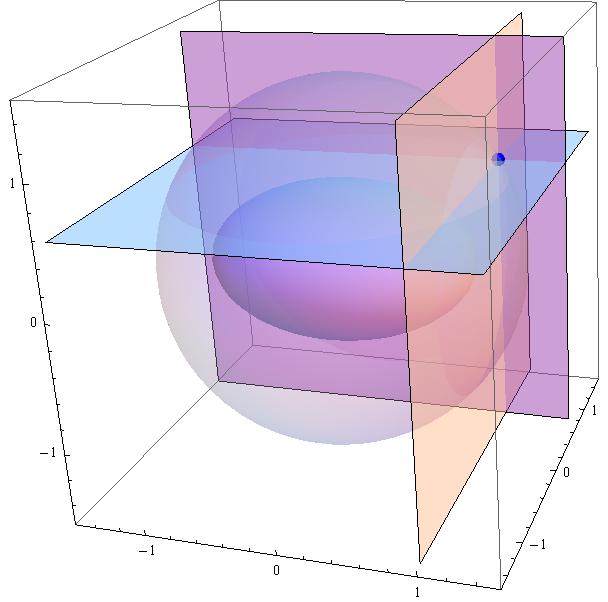
Attached a plot for the ellipsoid