Question

Show that the tangent to `f(x) = sinx` at `x=1` and the tangent to `g(x) = sin^-1x` at `y=1` are equally inclined to `y=x`?

Answer 1

It should be intuitive that this is true of any functions that fit this criteria as the functions are inverses and so reflected in the line `y=x`, and for all points, not just `x=1` for `f(x)` and `y=1` for `f^(-1)(x)`

In this specific case we can prove the result:

`f(x) = sinx`

Differentiating wrt `x` we have:

`f'(x) = cosx`

When `x=1 => f'(1) = cos1`

And for the inverse:

`g(x) = sin^-1(x)`

When `y=1 => g(x)=1`

`:. sin^-1(x) = 1`
`:. x = sin1`

Differentiating wrt `x` we have:

`g'(x) = 1/sqrt(1-x^2)`

And so, when `y=1` we have:

`g'(sin1) = 1/sqrt(1-sin^2 1)`
`g'(sin1) = 1/sqrt(cos^2 1)`
`g'(sin1) = 1/cos 1`

We can now calculate the inclinations of the tangents, Suppose:

the tangent line at `x=1` for `f(x)` is at an inclination of `alpha`
the tangent line at `y=1` for `g(x)` is at an inclination of `beta`
the tangent line of `y=x` is at an inclination of `pi/4`

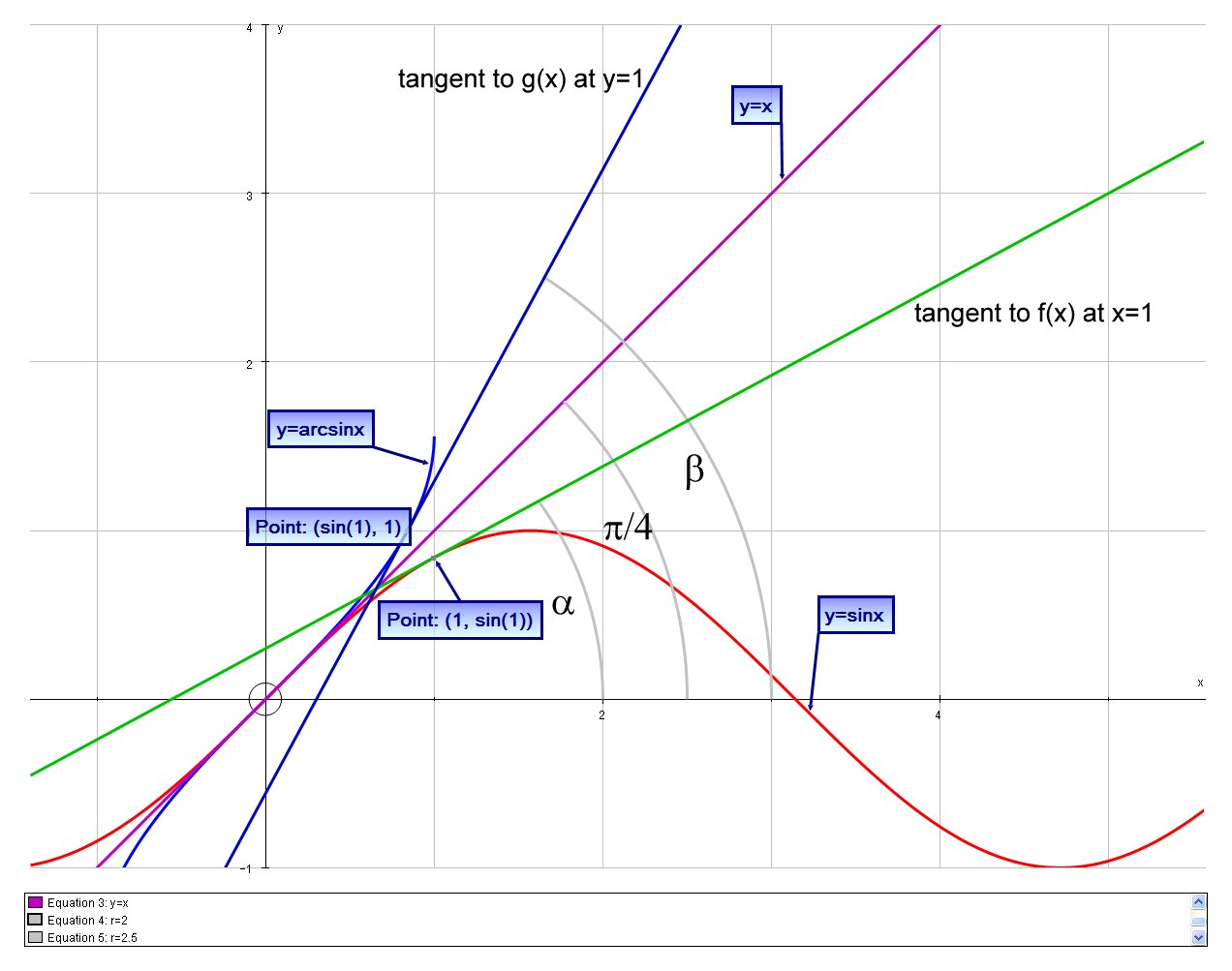
Then (by definition of the tangent and relation to the derivative), at those points;

`tan alpha = cos1`; `tan beta = 1/cos1` and `tan (pi/4) = 1`

So our aim is to show that the angle between one tangent and #y=x is the same as the other. ie that:

`beta - pi/4 = pi/4 - alpha => alpha + beta = pi/2`

Using `tan(A+B)=(tanA+tanB)/(1-tanAtanB)` we have:

`tan(alpha+beta) = (tanalpha+tanbeta)/(1-tanalphatanbeta)`
`" " = (cos1 +1/cos1)/(1-cos1 1/cos1)`
`" " = (cos1 +1/cos1)/0`
`" " = oo`

`:. alpha + beta = pi/2` QED

Or if you prefer, using `tan(A-B)=(tanA-tanB)/(1+tanAtanB)` we have:

`tan(beta-pi/4) = (tanbeta+tan(pi/4))/(1-tanbetatan(pi/4))`

`" " = (1/cos1-1)/(1+1/cos1)`

`" " = ((1-cos1)/cos1) / ((cos1+1)/cos1)`

`" " = (1-cos1) / (cos1+1)`

`tan(pi/4-alpha) = (tan(pi/4)-tanalpha)/(1+tan(pi/4)tanalpha)`

`" " = (1-cos1)/(1+cos1)`

`" " = tan(beta-pi/4)` QED