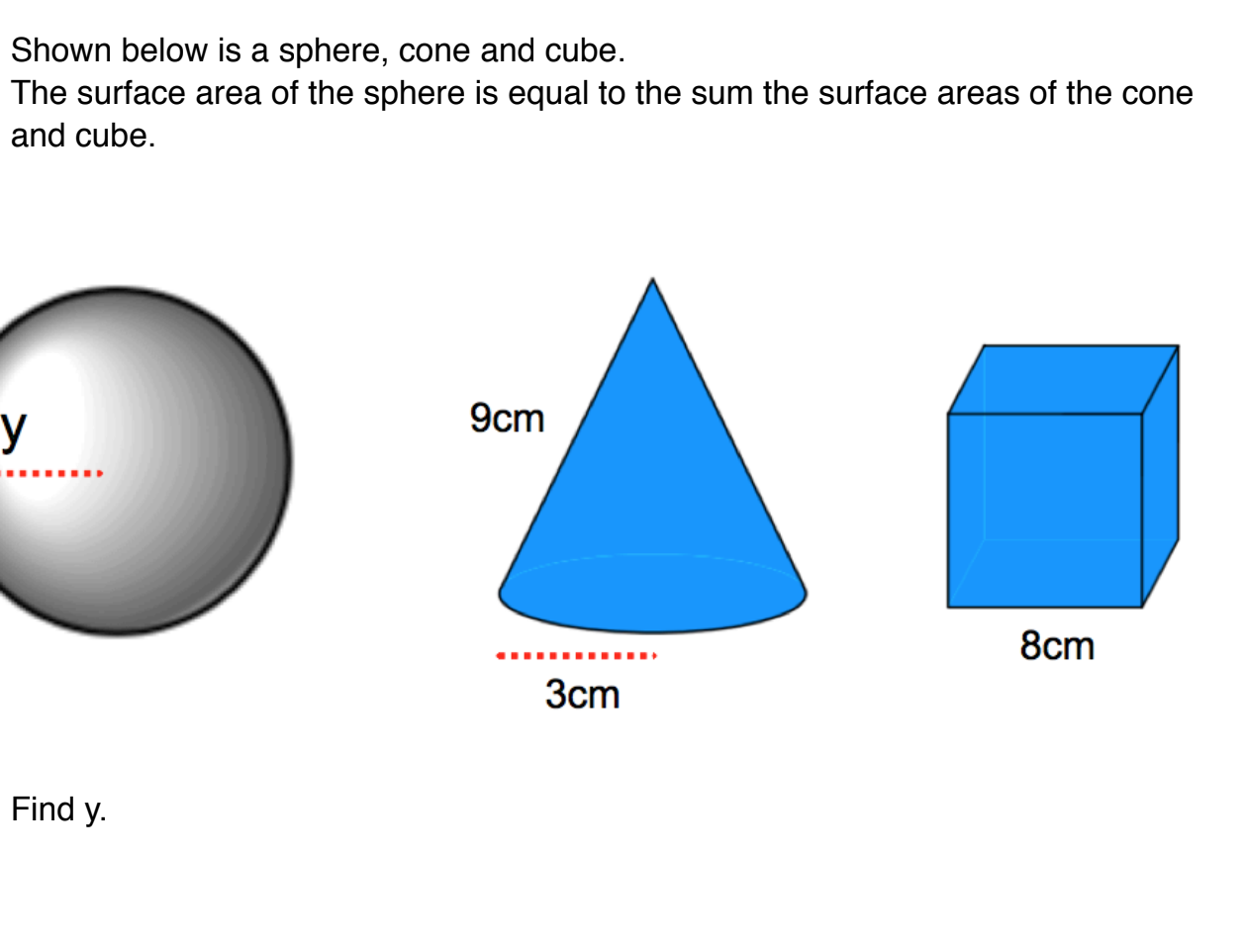
Shown below is a sphere, cone and cube. The surface area of the sphere is equal to the sum the surface areas of the cone and cube. so what is Y's number?

Question

2300 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-15T09:57:52

#color(blue)(y=r=sqrt(9+96/pi)~~6.2895)#

First calculate the surface areas of the cone and cube.

The surface area of the cube:

We have 6 faces each having a surface area of:

#8*8=64 "cm"^2#

Total surface area:

#6*64=384"cm"^2#

The surface area of a cone is given by:

#bb(A=pir(r+sqrt(h^2+r^2)))#

#h# is the height of the cone. We are given the length of the slope, so we will need to find #h#.

We can do this by using Pythagoras's theorem.

If the slope is the hypotenuse, and the radius is one of the sides of a right triangle, then the missing side #h# is:

#h=sqrt((9)^2-(3)^2)=sqrt(72)=6sqrt(2)#

Putting known values into the formula:

#A=pi(3)((3)+sqrt((6sqrt(2))^2+(3)^2))#

#A=pi(3)((3)+sqrt((72+9)))#

#A=pi(3)(12)=36pi#

Surface area of sphere is the sum of the surface area of the cube and the cone:

#(36pi+384) "cm"^2#

Surface area of a sphere is given by:

#bb(A=4pir^2)#

#:.#

#4pir^2=36pi+384#

We need to find #r# which will be our #y# value:

#4pir^2=36pi+384#

Divide by #4pi#:

#r^2=(36pi)/(4pi)+384/(4pi)#

#r^2=9+96/pi#

Taking square root:

#r=sqrt(9+96/pi)#

You can leave it in this form for an exact answer, or its approximate value of:

#color(blue)(y=r=sqrt(9+96/pi)~~6.2895)#