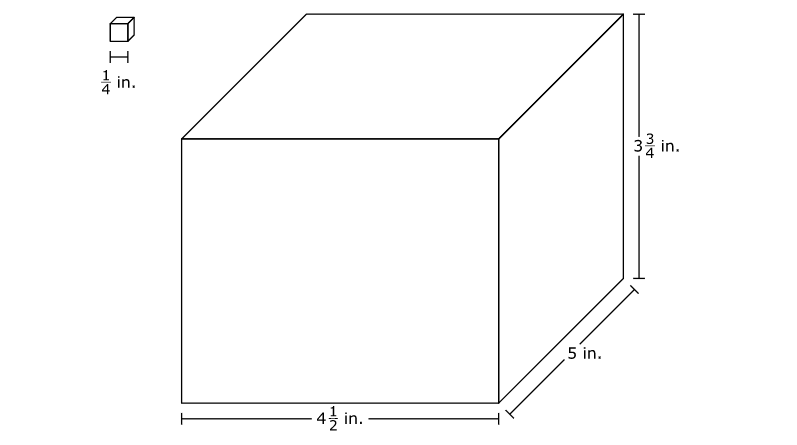
Small cubes with edge lengths of 1/4 inch will be packed into a rectangular prism (shown below). How many small cubes are needed to completely fill the rectangular prism?
Thank you for the answer!
Thank you for the answer!
2 Answers
it's a volume question
Explanation:
First, find the volume of the small shape.
Then, divide the volume of the bigger shape.
Finally, divide the big shape volume by the small shape volume.
Smaller shapes will fit into bigger shapes.
5400
Explanation:
Using a word incorrectly for mathematics; it is a matter of how many 'towers' of
Consider the height of one 'tower'
Height
Consider the 5 inches depth
Consider the
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
One approach for working it out without a calculator.
Using a calculator is much easier.
Note that 20 is the same as
Total count of 'towers'
Total count of blocks at 15 per 'tower'
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
What follows is just a way of thinking!



