By definition,
#lim_(xrarrcolor(green)(a))color(red)(f(x)) = color(blue)(L)# if and only if
for every #epsilon > 0#, there is a #delta > 0# such that:
for all #x#, #" "# if #0 < abs(x-color(green)(a)) < delta#, then #abs(color(red)(f(x))-color(blue)(L)) < epsilon#.
So we want to make #abs(underbrace(color(red)"function")_(color(red)(f(x)) )-underbrace(color(blue)("number"))_color(blue)(L))# less than some given #epsilon# and we control (through our control of #delta#) the size of #abs(x-underbrace(color(green)((a)))_color(green)(a))#
To find #delta#, look at the thing you want to make small, #abs(f(x)-L)# and try to rewrite it so that you see the thing that you control #abs(x-a)#
If we can get #abs(f(x)-L) = abs(c)abs(x-a)# then
making #delta # and consequently #abs(x-a)# less that #epsilon/abs(c)#
will get us #abs(f(x)-L)# is less that #epsilon#
So the answer to the first question is
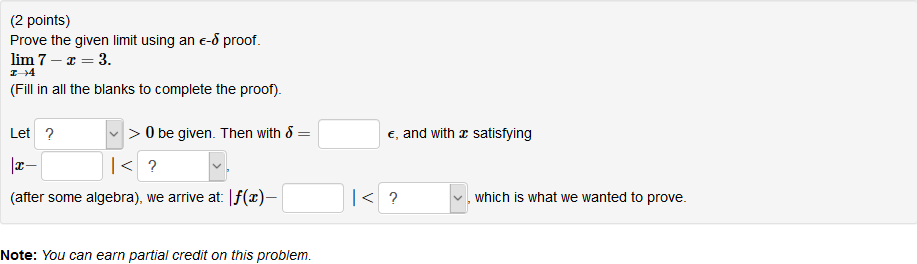
Let #color(blue)epsi##> 0# be given. Then with #delta = 1 # #epsilon#, and with #x# satisfying #abs(x-color(blue)4)##< color(blue)delta#, (after some algebra), we arrive at #abs(f(x)-color(blue)(3)) < color(blue)epsilon#
Important note: The fill-in-the-blank statement supplied in your answer is incomplete compared to the definition of limit.
The inequality that #x# should satisfy should be
with #x# satisfying #color(red)(0 < )abs(x-color(blue)4)##< color(blue)delta#