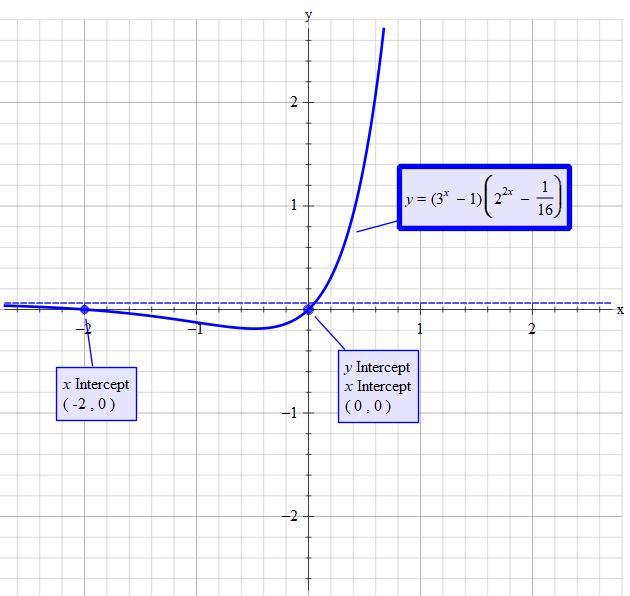
Solve #(3^x - 1)(2^(2x) - 1/16) = 0# for x?

Question

1429 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-08-27T14:26:12

#x=-2#
#x=0#

#color(blue)("Determine the first root")#

Before we start: #log(a^b)# is the same as #blog(a)#

Divide both sides by #(3^x -1)#

Note that #0/(3^x-1)=0#

#2^(2x)-1/16=0#

#2^(2x)=1/16#

Take logs of both sides. I choose #log_10#

#2xlog(2)=log(1/16)#

#x=(log(1/16))/(2log(2))#

#x=-2#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Check
#(3^x - 1)(2^(2x) - 1/16) = 0" " ->" " (3^(-2)-1)(2^(2xx(-2))-1/16)=0#

#color(white)("bbbbbbbbbbbbbbbbbbbbbs") ->" "-8/9(1/16-1/16)=0#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the second root")#

Set #(3^x-1) =0#

#3^x=1#

but as #3^0=1# we must have

#x=0#

Tony B