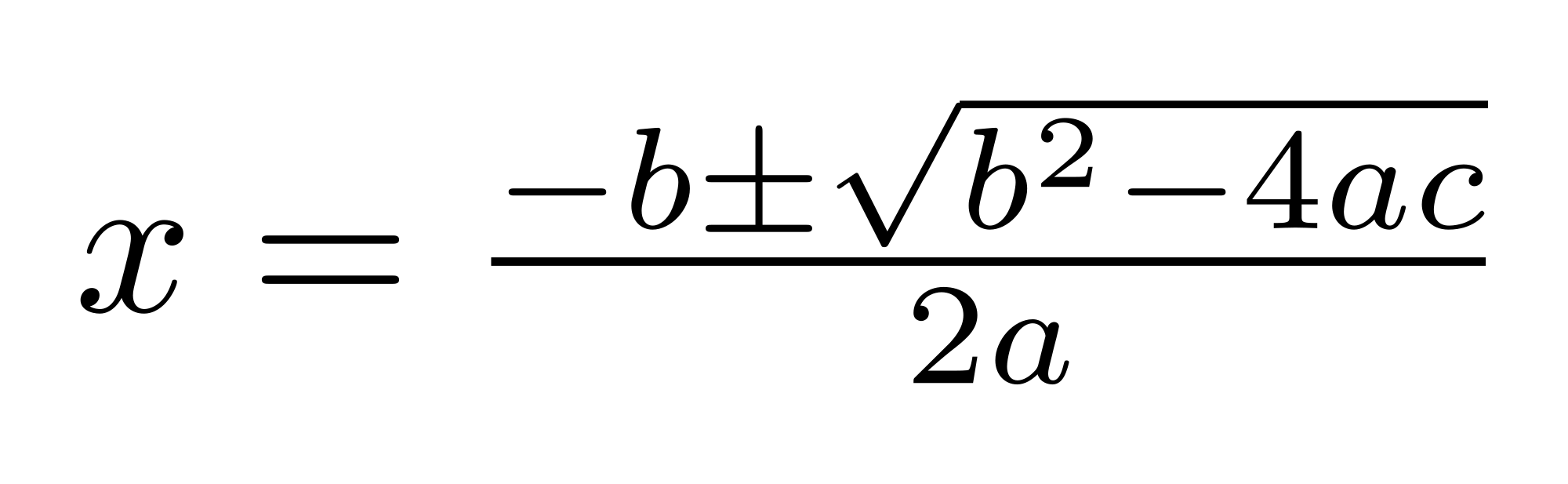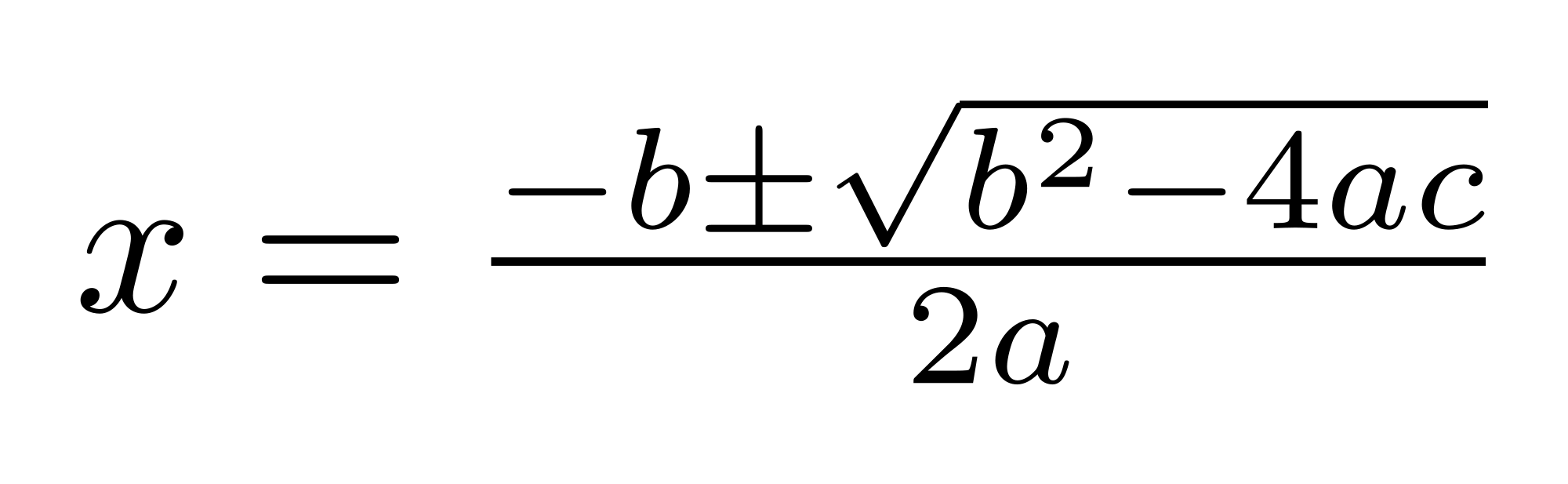The quadratic formula states:
For #color(red)(a)x^2 + color(blue)(b)x + color(green)(c) = 0#, the values of #x# which are the solutions to the equation are given by:
#x = (-color(blue)(b) +- sqrt(color(blue)(b)^2 - (4color(red)(a)color(green)(c))))/(2 * color(red)(a))#
Substituting:
#color(red)(3)# for #color(red)(a)#
#color(blue)(4)# for #color(blue)(b)#
#color(green)(10)# for #color(green)(c)# gives:
#x = (-color(blue)(4) +- sqrt(color(blue)(4)^2 - (4 * color(red)(3) * color(green)(10))))/(2 * color(red)(3))#
#x = (-color(blue)(4) +- sqrt(16 - 120))/6#
#x = (-color(blue)(4) +- sqrt(-104))/6#
#x = (-color(blue)(4) +- sqrt(4 xx -26))/6#
#x = (-color(blue)(4) +- sqrt(4)sqrt(-26))/6#
#x = (-color(blue)(4) +- 2sqrt(-26))/6#