Solve equation: (Is my answer correct ?)
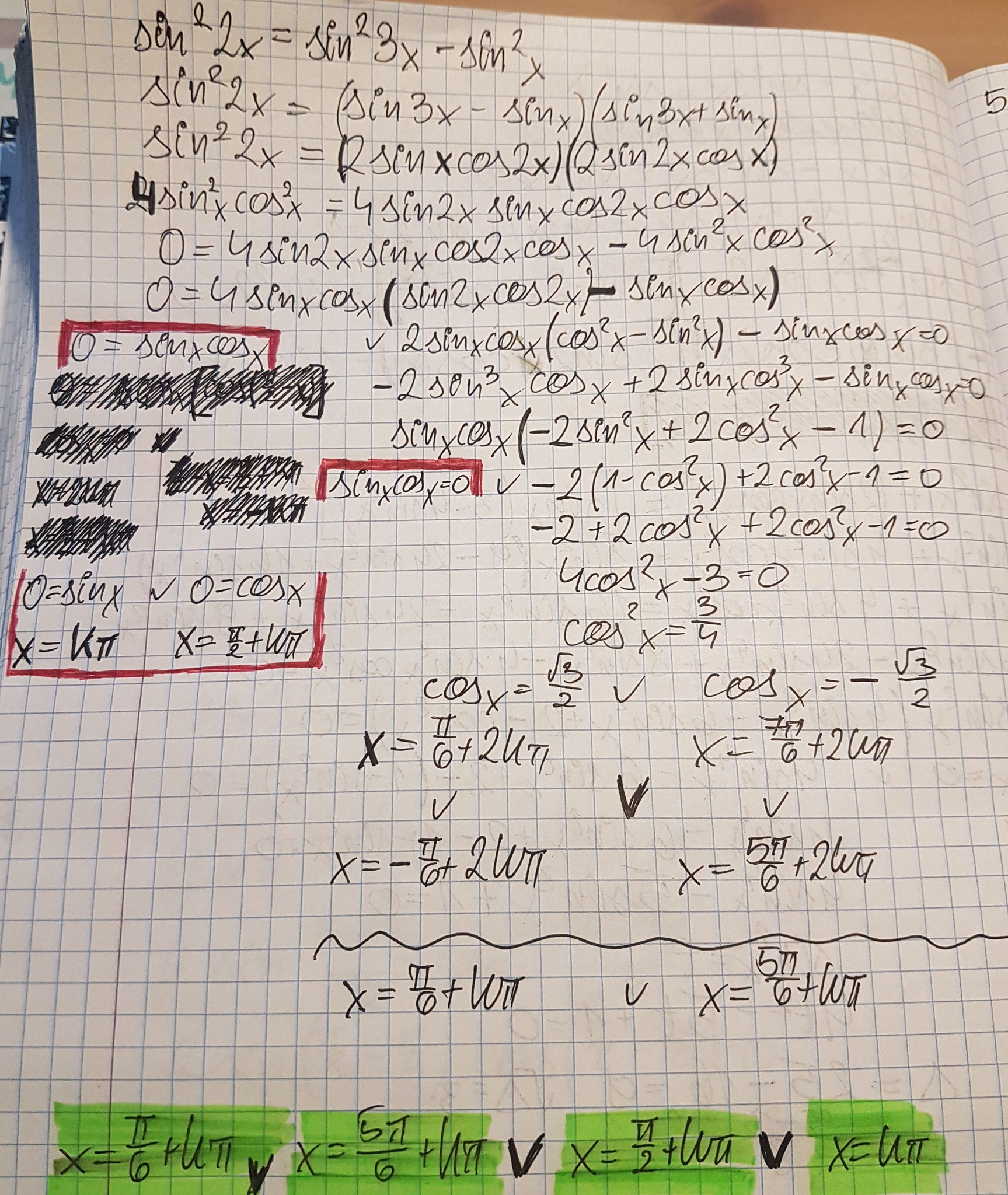
1 Answer
Jun 27, 2018
Explanation:
Develop the right side:
RS = (sin 3x - sin x)(sin 3x + sin x)
RS = (2cos 2x.sin x)(2sin 2x.cos x) = (2sin x.cos x)(2sin 2x.cos 2x)=
RS = sin 2x.sin 4x
Equation (1) becomes:
Either factor should be zero.
a. sin 2x = 0. Unit circle gives:
b.
Unit circle gives:
1.
2.
