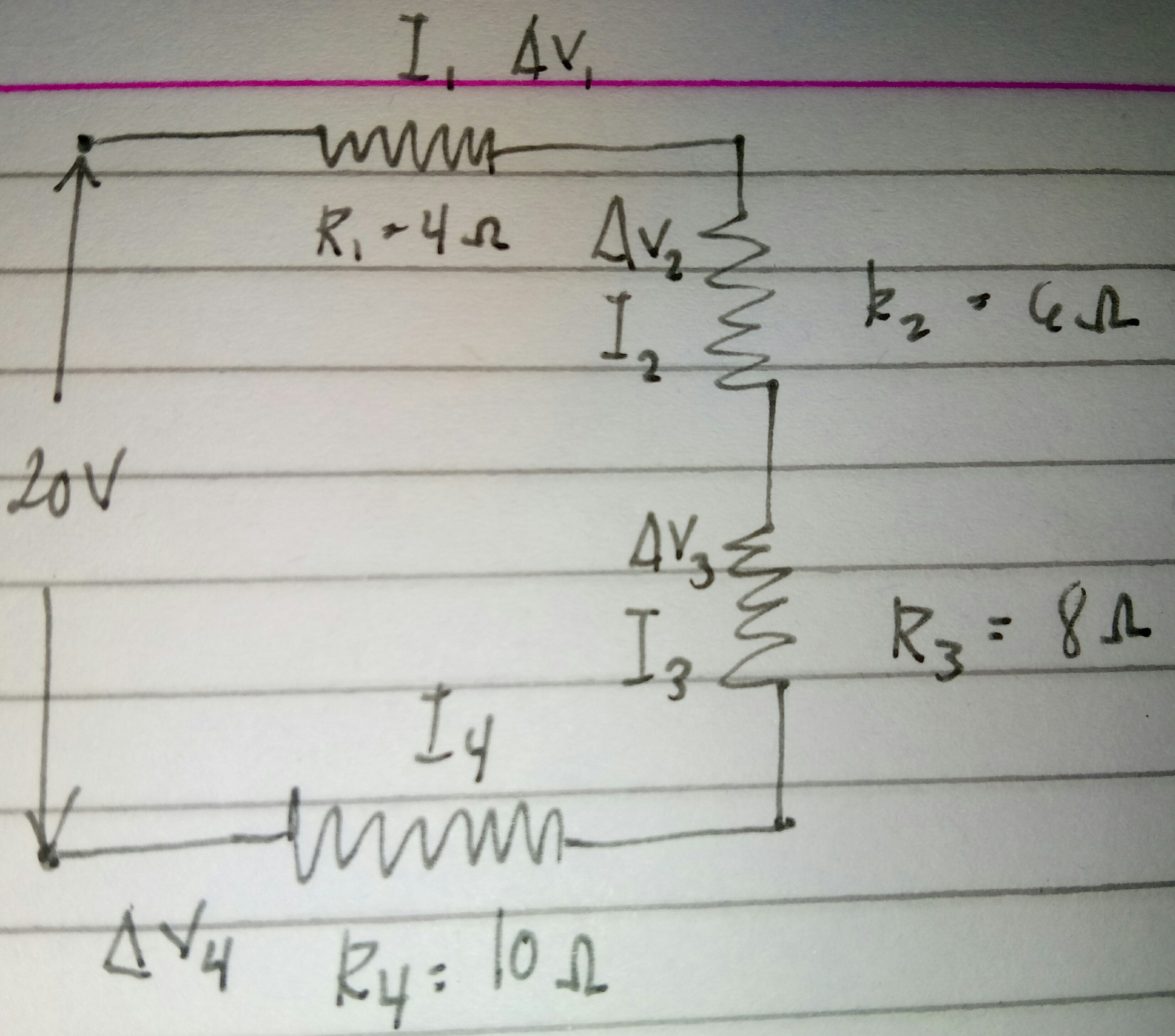
As all the resistors R_1, R_2, R_3 and R_4 are in series, the same amount of current will flow through all. Let this current be I
therefore I = I_1=I_2=I_3=I_4
To calculate I, we must first calculate the equivalent resistance between the two terminals.
For a series circuit, R_eq = R_1+R_2+ R_3 + R_4
R_(eq) = 4+6+ 8+ 10= 28 Omega
As total voltage applied across the circuit is 20V,
The current I can be calculated as:
I = V/R = 20/28 = 5/7 = 0.7142857 A approx 71.4 mA
SO, current through every resistor will be same = 71.4 mA or 0.714 A
Now we can calculate the voltage drop and power across each resistor:
V_1 = I xx R_1 = 0.714 xx 4= 2.856 V and
P_1 = V_1^2 / R_1 = 2.856^2 / 4 =2.039184 W
V_2 = I xx R_2 = 0.714 xx 6= 4.284 V and
P_2 = V_2^2 / R_2 = 4.284^2 / 6 =3.058776 W
V_3 = I xx R_3 = 0.714 xx 8= 5.712 V and
P_3= V_3^2 / R_3 = 5.712^2 / 8 = 4.078368 W
V_4 = I xx R_4 = 0.714 xx 10= 7.14 V and
P_4= V_4^2 / R = 7.14^2 / 10 =5.09796 W
I_1=I_2=I_3=I_4 = 0.714 A
V_1 = 2.856 V; P_1 = 2.039184 W
V_2 = 4.284 V ; P_2 = 3.058776 W
V_3 = 5.712 V; P_3= 4.078368 W
V_4 = 7.14 V And P_4 = 5.9296 W
Note : A = amperes
V= Volts and W = Watts.