Question

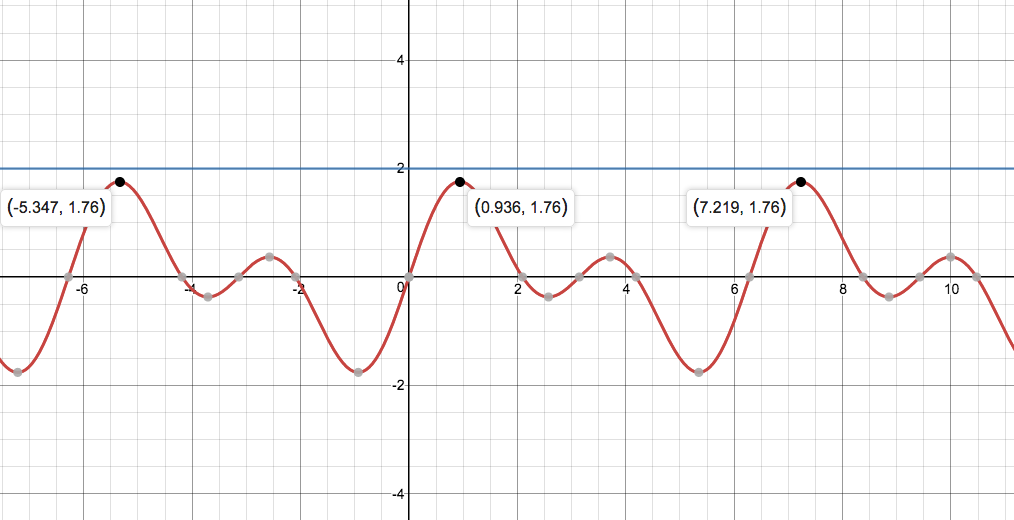
Solve the ecuation sinx+sin2x=2?

Answer 1

No solutions for `x in RR`

i.e. no solutions for real values of `x`

Explanation:

This is a rather interesting problem, one of the most standard tricks in trig, is to recognise the use `sin2theta -= 2sintheta costheta`
But in this problem this simply will be very difficult

We may first need to do some differential calculus, to find the maximum:

let `y = sinx + sin2x`

Then we can differentiate:

`(dy)/(dx) = cos + 2cos2x`

For stationary: `(dy)/(dx) = 0`:

`cosx + 2cos2x = 0`

Using identities:

`cosx + 2(2cos^2 x -1 ) = 0`

`cosx + 4cos^2 x -2 = 0`

`=> 4cos^2x + cosx - 2 = 0`

Treating this like a quadratic, and using the quadratic formula:

`cos x = {(-1+sqrt(33) ) / 8 , -(1+sqrt(33)) / 8 }`

`=> x = {0.936 , 5.347 , 2.574 , 3.710 }`

Now trying all the `x's` we just obtained for our stationary point, we see that the maximum point for `y` is `(0.936, 1.76 )`

So hence `sinx + sin2x` is never equal to 2:

No solutions: `->` as scene below, the never intersect...