Solve the polynomial inequality and express in interval notation? #x^2-2x-15<0#
the solution is shown as (-3,5) but why does this problem not use negative infinity or infinity? is there something i'm missing?
the solution is shown as (-3,5) but why does this problem not use negative infinity or infinity? is there something i'm missing?
1 Answer
A parabola that opens upward can only be less than zero in the interval between the roots.
Explanation:
Please observe that the coefficient of the
graph{y = x^2-2x-15 [-41.1, 41.1, -20.54, 20.57]}
Please look at the graph and observe that a parabola that opens upward can only be less than zero in the interval between but not including the roots.
The roots of the equation
The value of the quadratic is less than zero between these two numbers,
Please look at the graph:
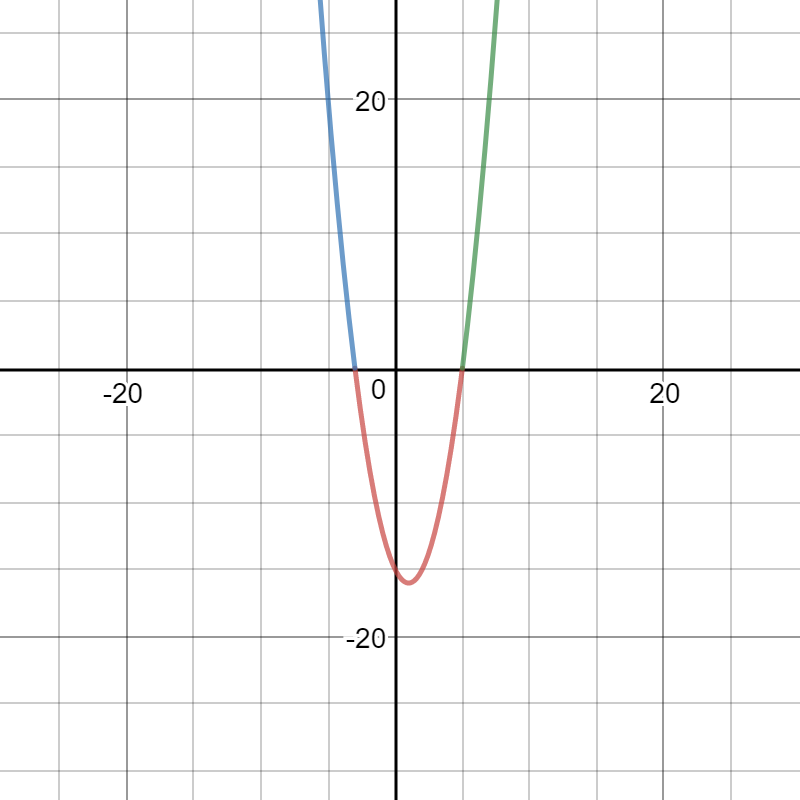
The region in red is the region where the values of y are less than zero; the corresponding x values is the region between the two roots. This is always the case for a parabola of this type. The region in blue contains the y values where the corresponding x values would contain
When you have a parabola that opens upward and the parabola has roots, the region between the two roots is the region that is less than zero; the domain of this region is NEVER bounded by
