Question

Solve this?

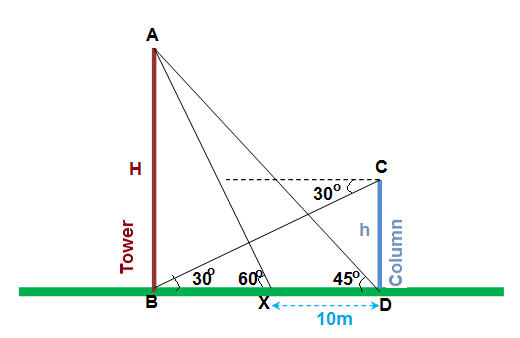
From the foot of a column the angle of elevation of the top of a tower is 45° and from the top of column the angle of depression of the bottom of the tower is 30°. A man walks 10 meters from the bottom of the column towards the tower. He notices the angle of elevation of its top to be 60°. Find the heights of the column and the tower.

Answer 1

In `Delta ABD,angle ADB=45^@`

So the triangle is right isosceles

and `BD=AB=H= " Height of the tower"`

Now `(AB)/(BX)=tan60^@`

`=>(AB)/(BD-DX)=sqrt3`

`=>H/(H-10)=sqrt3`

`=>H=(H-10)sqrt3`

`=>H=(10sqrt3)/(sqrt3-1)=(10sqrt3)/2xx(sqrt3+1)=15+5sqrt3`m

Now `(CD)/(BD)=tan30^@`

`=>h/H=1/sqrt3`

`=>h=H/sqrt3=(15+5sqrt3)/sqrt3=5sqrt3+5` m