Solve this quadratic equation. Return the answer in 2 decimals ?
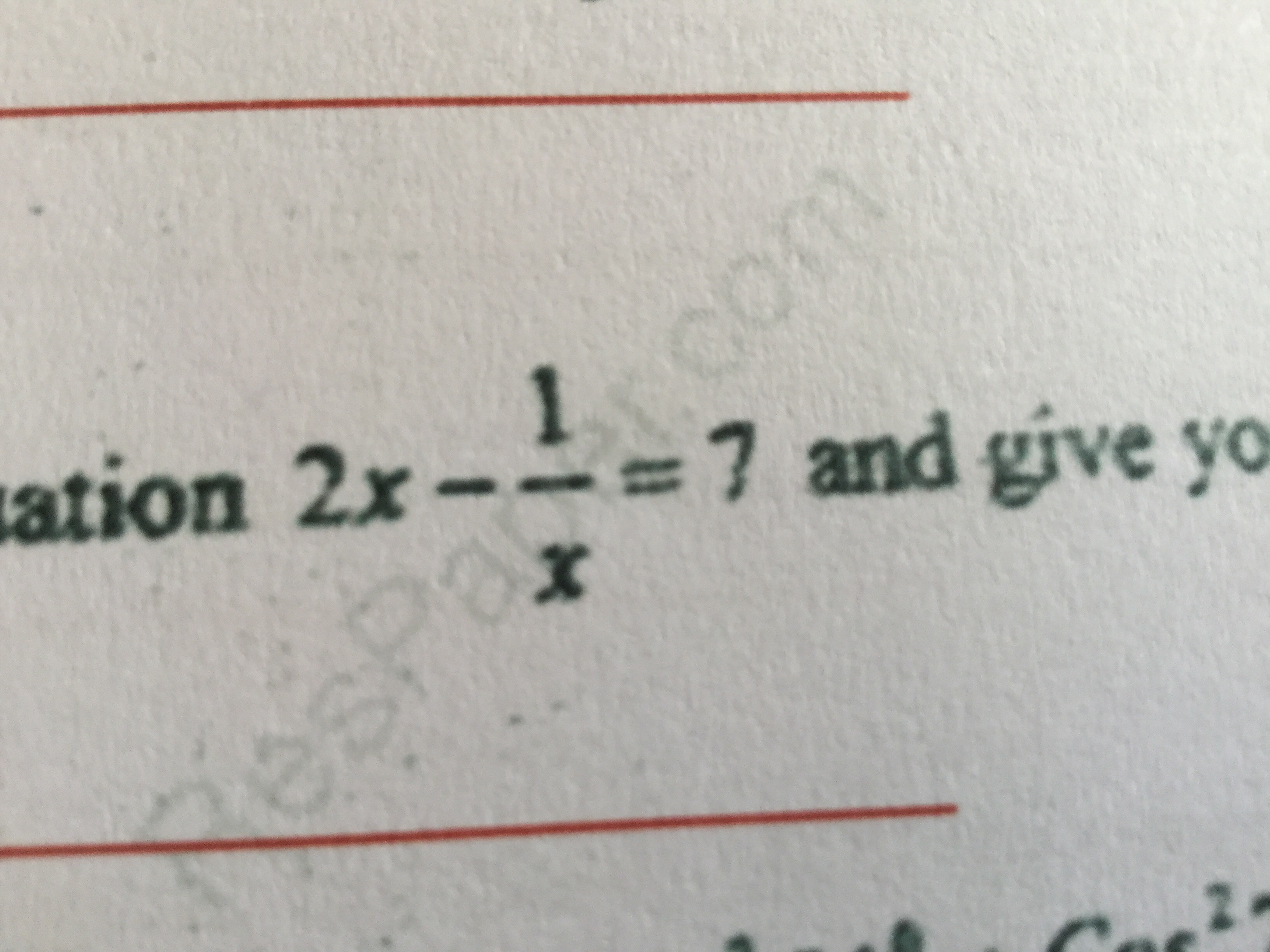
3 Answers
Explanation:
We have
Multiplying both sides by
Now we have a quadratic equation. For any
Here,
We can input:
Explanation:
This is clearly not a comfortable form to work with.
Multiply through by
See below...
Explanation:
First we need the standard format of
First we multiply all by
Now we move the
As we want the answers to
We know that
Now from our equation we know that ...
Now we plug these into our formula, but as we have a
Now we put each one into our calculator and round to
Both to



