Given: #x^3+x^2-7x+2=0#
#color(blue)("Step 1")#
Consider the constant of 2.
The whole number factors are #1,-1,2,-2#
Test #x=1#
#1^3+1^2-7(1)+2!=0#
Test #x=2#
#2^3+2^2-7(2)+2#
#8+4-14+2=0# so #x=2# is a factor giving:
#(x-2)(?x^2+?x-1)#
It has to be (-1) as #(-2)xx(-1)=+2#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Step 2 - consider the final "x^3" term")#
We require the first term to be #x^3# so the structure has to be:
#(color(red)(x-2))(x^2+.........-1)#
#color(red)(x) xx x^2=x^3# so that is ok!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Step 3 - consider the final "x^2" term")#
The negative 2 in the first bracket gives
#color(red)(-2)xx x^2 = -2x^2#
But we need to have #+x^2# so we need to 'build' #+3x^2# to compensate as #+3x^2-2x^2=x^2#
#color(red)(x)color(green)(xx3x)# should do it giving:
#(color(red)(x-2))(x^2color(green)(+3x)+.........-1)#
So what have we got now?
#(color(red)(x-2))(x^2+3x+......-1) -> x^3+3x^2-2x^2-6x -1 #
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Step 4 - consider the final "x" term")#
The target is #-7x# and we have #-6x# so we need another #-x#
So far we have not included the #-1# in the last bracket. lets do so:
Test:
#color(red)((x-2))(x^2+3x-1)#
#color(white)(-)color(red)(x)(x^2+3x-1) color(white)("d")->color(white)("d") x^3+3x^2-x+0#
#color(white)("d")color(red)(-2)(x^2+3x-1)color(white)("d")->ul(color(white)("d.")0-2x^2-6x+2 larr" Add")#
#color(white)("dddddddddddddddddddd")x^3+x^2-7x+2 larr" As required"#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Step 5 - Solving for = 0")#
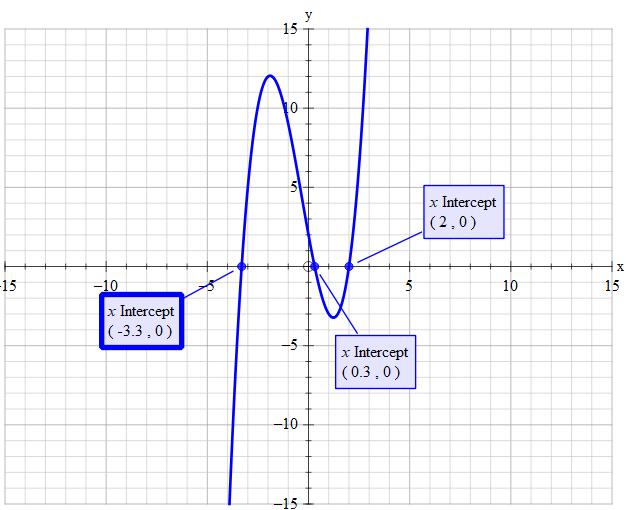
Set #color(red)(x-2)=0 => x=+2#
Set #x^2+3x-1=0#
#x=(-3+-sqrt(3^2-4(1)(-1)))/2#
#x=-3/2+-sqrt(13)/2#
#x~~ +0.3028# to 4 dp
#x~~-3.3028# to 4 dp