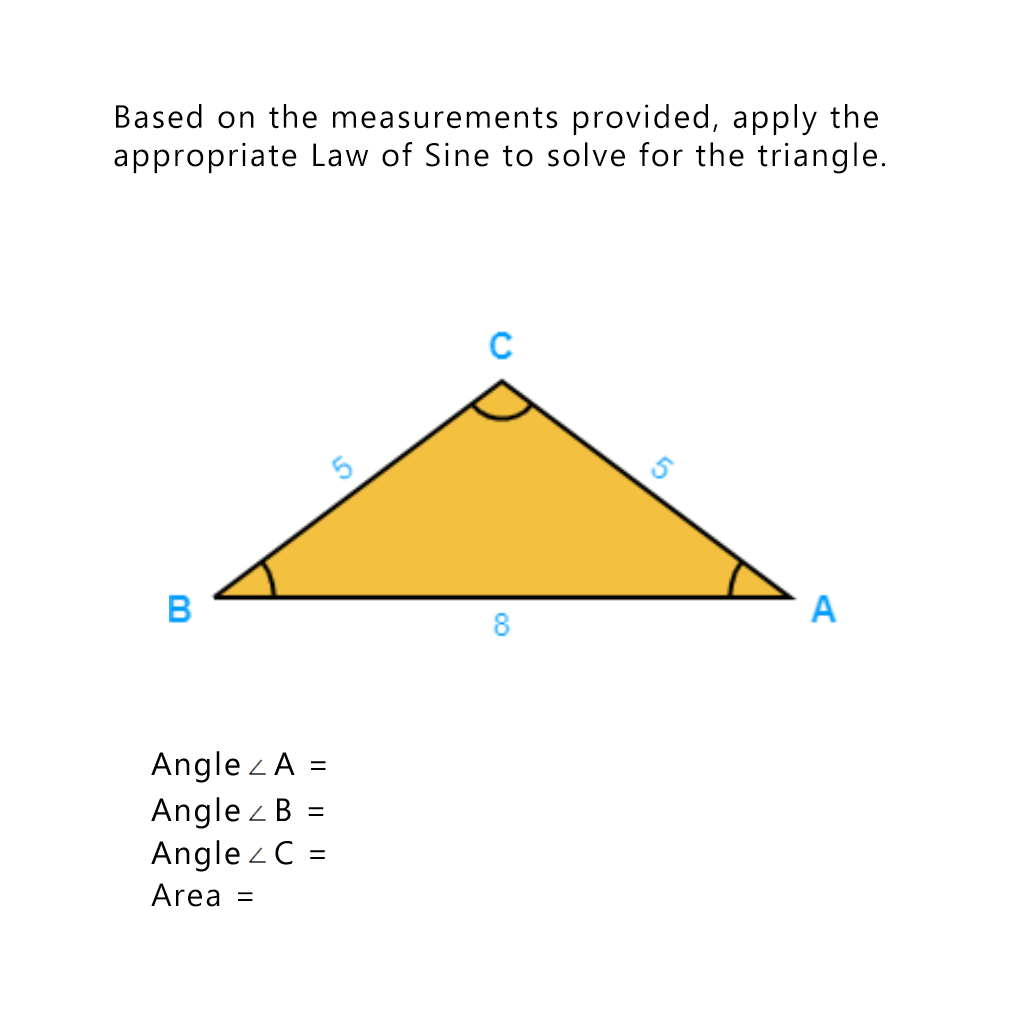
From the image :
#BC=CA=5 and AB=8#
#angleA=angleB=>color(green)(triangle ABC " is isosceles triangle."#
Also, #A+B+C=180^circ=>color(violet)(B and C " are acute angles."#
#=>a=5,b=5, andc=8#
#:."perimeter " : 2s=a+b+c=5+5+8=18#
#:.s=9=>s-a=4,s-b=4 and s-c=1#
#:." area of triangle"=Delta=sqrt(s(s-a)(s-b)(s-c))#
#=>color(brown)(Delta=sqrt(9(4)(4)(1))=sqrt144=12#
Now , we know that , # Delta=(abc)/(4R)=>R=(abc)/(4Delta)#
#:.R=(5xx5xx8)/(4xx12)=25/6#
#"Using "color(blue)"sine rule:"#
#color(blue)(a/sinA=b/sinB=c/sinC=2R#
#:.sinA=a/(2R)=5/(2xx(25/6))=30/50=0.6#
#:.angle A=arcsin(0.6)#
#=>color(red)(angleA=(36.87)^circ#
#=>color(red)(angleB=(36.87)^circ......to[becauseangleA=angleB]#
We have , #A+B+C=180^circ=>C=180^circ-(A+B)#
#:.C=180^circ-(36.87+36.87)^circ=180^circ-(73.74)^circ#
#:.color(red)(angle C=(106.26)^circ#
Hence,
#angle A=(36.87)^circ ,angle B=(36.87)^circ ,angle C=(106.26)^circ #
#" area of triangle"=Delta=12 " sq. units"#