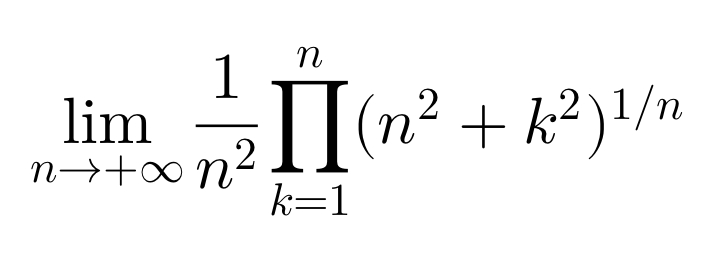The number one most important identity for solving any kind of problem with infinite product is converting it into a problem of infinite sums:
\prod_{k=1}^{n}a_k = a_1 * a_2 * a_3 ... = e^{ln(a_1)} * e^{ln(a_2)} * e^{ln(a_3)} ...
EMPHASIS:
= exp[\sum_{k=1}^{n}ln(a_k)]
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
But, before we can do this, we must first deal with the #\frac{1}{n^2} in the equation and btw let's called the infinite product L:
L = \lim_{n\to +\infty} \frac{1}{n^2}\prod_{k=1}^{n} (n^2 + k^2)^{\frac{1}{n}}
= \lim_{n\to +\infty} \frac{1}{n^2}\prod_{k=1}^{n} [n^2 (1+ \frac{k^2}{n^2})]^{\frac{1}{n}}
= \lim_{n\to +\infty} \frac{n^2}{n^2}\prod_{k=1}^{n} (1+ \frac{k^2}{n^2})^{\frac{1}{n}}
= \lim_{n\to +\infty} \prod_{k=1}^{n} (1+ \frac{k^2}{n^2})^{\frac{1}{n}}
Now we can convert this into an infinite sum:
L = \lim_{n\to +\infty} \prod_{k=1}^{n} (1+ \frac{k^2}{n^2})^{\frac{1}{n}}
= \lim_{n\to +\infty} exp[\sum_{k=1}^{n}ln((1+ \frac{k^2}{n^2})^{\frac{1}{n}})]
apply logarithm properties:
L = \lim_{n\to +\infty} exp[\sum_{k=1}^{n} \frac{1}{n} * ln(1+ \frac{k^2}{n^2})]
And using limit properties:
L = exp[\lim_{n\to +\infty} \sum_{k=1}^{n} \frac{1}{n} * ln(1+\frac{k^2}{n^2})]
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let's call the infinite sum S:
S = \lim_{n\to +\infty} \sum_{k=1}^{n} \frac{1}{n} * ln(1+ \frac{k^2}{n^2})
And keep in mind that
L = exp(S)
Now let's solve your question by converting it from a RIEMANN SUM to a DEFINITE INTEGRAL:
Recall the definition of a Riemann sum is :
EMPHASIS:
\int_{a}^{b}f(x)dx = \lim_{n\to +\infty}\sum_{k=1}^{n}f(a+k(\frac{b-a}{n})) * \frac{b-a}{n}
Let
\lim_{n\to +\infty}\sum_{k=1}^{n}f(a+k(\frac{b-a}{n})) * \frac{b-a}{n} = \lim_{n\to +\infty} \sum_{k=1}^{n} \frac{1}{n} * ln(1+ \frac{k^2}{n^2}) = S
Now, let f(x) = ln(1+x^2) and a = 0
f(k(\frac{b}{n})) =ln(1+ \frac{k^2}{n^2})
Thus, b = 1 i.e.
f(\frac{k}{n}) = ln(1+ \frac{k^2}{n^2})
Therefore,
S = \lim_{n\to +\infty} \sum_{k=1}^{n} \frac{1}{n} * ln(1+ \frac{k^2}{n^2}) = \int_{0}^{1}ln(1+x^2)dx
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Solve for \int_{0}^{1}ln(1+x^2)dx :
use integration by parts:
\int uv dx = u\int v dx - \int (u' * \int vdx)dx
Let u = ln(1+x^2) and v = 1
Then, use chain rule and the derivative of natural logarithm to get u' = 1/(1+x^2) * 2x = \frac{2x}{1+x^2}
and use power rule to get: \int 1dx = x
\int ln(1+x^2)dx = ln(1+x^2) * x - [ \int (\frac{2x}{1+x^2} * x)dx]
= ln(1+x^2) * x - [ \int \frac{2x^2}{1+x^2}dx]
= xln(1+x^2) - 2[ \int \frac{x^2}{1+x^2}dx]
= xln(1+x^2) - 2[ \int \frac{x^2+1 -1}{x^2 + 1}dx] Use subtraction rule:
= xln(1+x^2) - 2[ \int \frac{x^2+1}{x^2 + 1} - \int \frac{1}{x^2 + 1} dx]
= xln(1+x^2) - 2[ \int1 - \int \frac{1}{x^2 + 1} dx]
Use power rule for the first integral and the second integral is the standard trigonometric function arctan(x) (the inverse of the tangent function)
= xln(1+x^2) - 2[ x - arctan(x)]
Thus, \int ln(1+x^2)dx = xln(1+x^2) - 2x + 2 arctan(x) + C
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now solve for the definite integral:
S = \int_{0}^{1}ln(1+x^2)dx
we know that the anti-derivative is F(x) = xln(1+x^2) - 2x + 2 arctan(x) + C, Thus
S = F(x) |_{x=0}^{x=1} = F(1) - F(0)
S = 1ln(1+1^2) - 2(1) + 2 arctan(1) - 0 + 0 - arctan(0)
note that arctan(1) is 45° or \frac{\pi}{4} (recall the special right triangle with side lengths 1,1, \sqrt{2} and angles 45°,45°,90°) and also arctan(0) = 0
Thus S = ln(2) - 2 + 2 (\frac{\pi}{4}) = ln(2) - 2 + \frac{\pi}{2}
or \approx 0.263943507354...
L = exp[S]= exp[ln(2) - 2 + \frac{\pi}{2}] = e^{ln(2)} * e^{-2} * e^{\frac{\pi}{2}}
L = 2 * \frac{1}{e^2} * (e^{pi}) ^ {1/2}
L = \frac{2\sqrt{e^pi}}{e^2}
Therefore the solution is \lim_{n\to +\infty} \frac{1}{n^2}\prod_{k=1}^{n} (n^2 + k^2)^{\frac{1}{n}} = \frac{2\sqrt{e^pi}}{e^2} or \approx 1.302054638...