Question

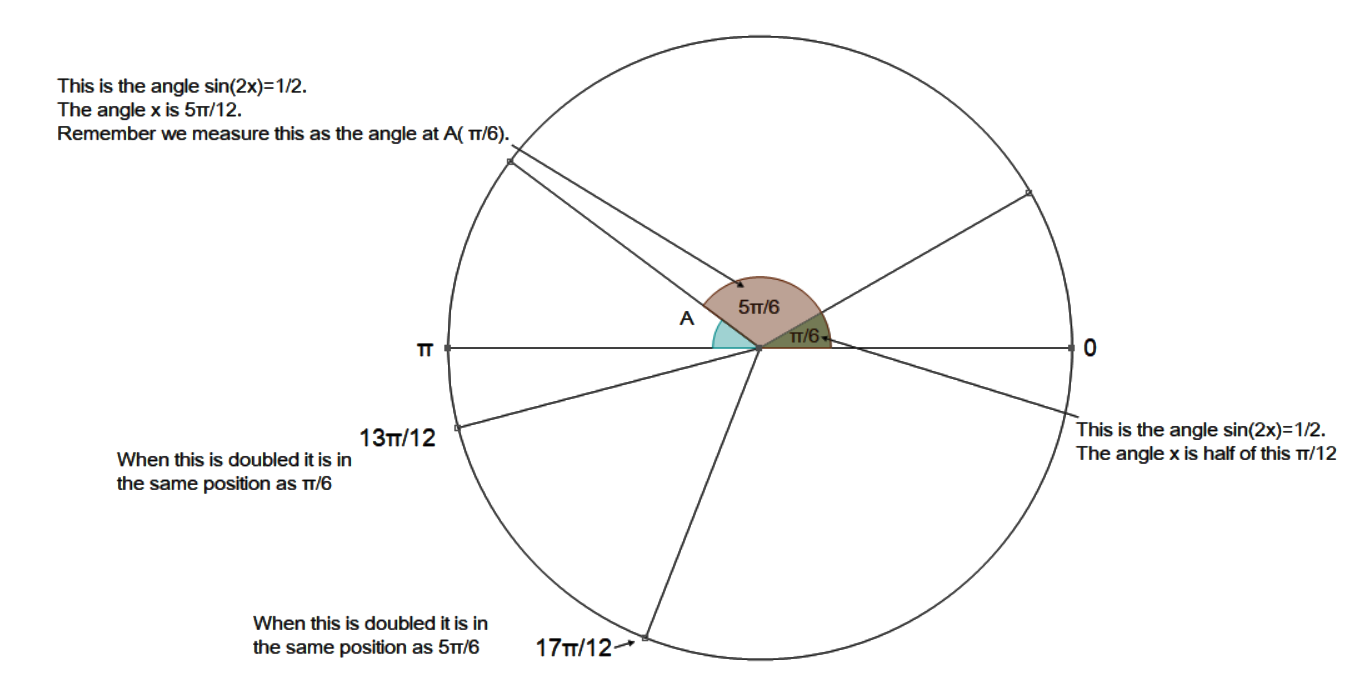
Solving Trigonometric Equations. Solve algebraically sin2x=0.5, 0<x<2pi?

I only got pi/12 and 5pi/12, but the answer key says that 13pi/12 and 17pi/12 are also answers. Please explain how to get these other two answers.

Answer 1

See below.

Explanation:

`sin(2x)=1/2`

`arcsin(sin(2x))=arcsin(1/2)`

`2x= pi/6, (5pi)/6 , (13pi)/6, (17pi)/6`

`x=pi/12 , (5pi)/12,(13pi)/12, (17pi)/12`

The missing values are just:

`2x=(pi)/6+2pi=(13pi)/6` , `x=(13pi)/12`

`2x=(5pi)/6+2pi=(17pi)/6` , `x=(17pi)/12`

All that has happened is we have gone round another rotation, i.e. `2pi`. This is valid because `x` is still in the interval `0 < x< 2pi`

This can often catch you out. You just need to remember that you have the ratio of `2x` not `x`.

Maybe this will help. I think what is confusing you is the fact that `(13pi)/12` and `(17pi)/12` are in the III quadrant, and as you found out have negative ratios. When these are multiplied by `2` they are then in the I and II quadrants which will then have positive ratios. Our problem only stated that twice the angle had a ratio of `1/2`, but `x` just had to be in the interval `0 < x<2pi`. All the angles are in this interval.