Question

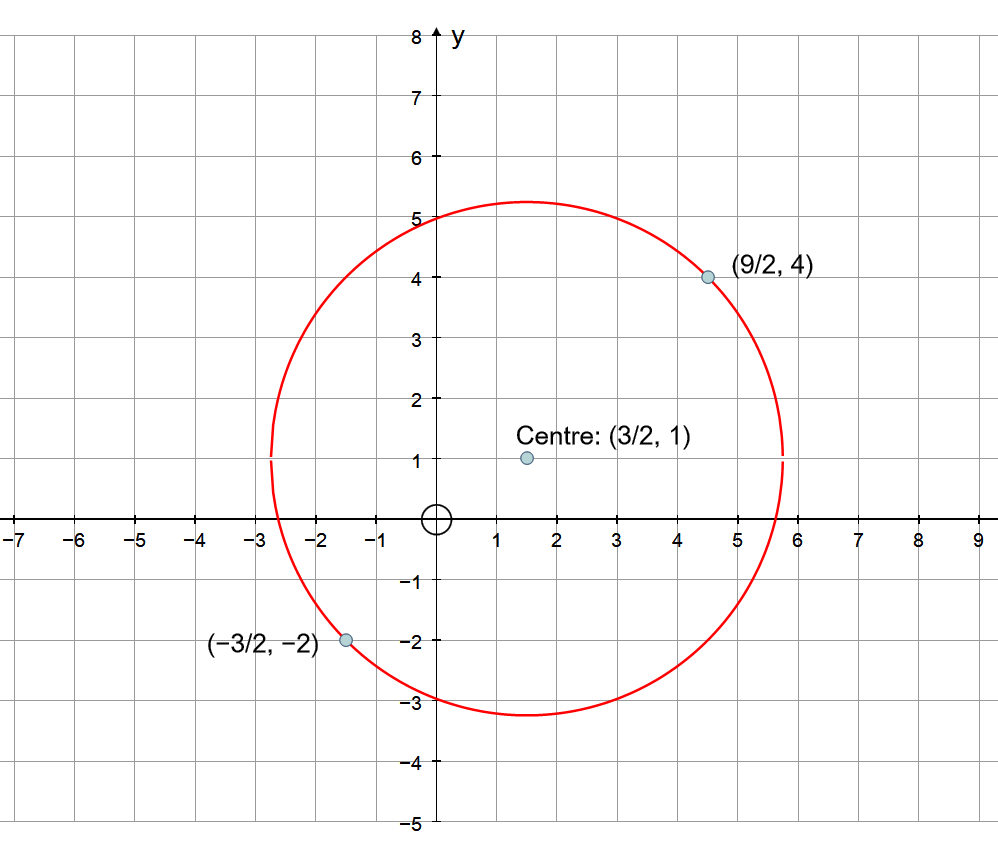
Standard equation of a circle which has a diameter with endpoints (9/2,4) and (-3/2,-2)?

Answer 1

`color(blue)((x-3/2)^2+(y-1)^2=18)`

Explanation:

The standard equation of a circle is given as:

`(x-h)^2+(y-k)^2=r^2`

Where `bbh` and `bbk` are the `bbx` and `bby` coordinates of the centre respectively and `bbr` is the radius.

We are given the end points of the diameter. If we find the distance between the end points and halve this, this will give us the radius:

Using the distance formula:

`|d|=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

`|d|=sqrt((9/2-(-3/2))^2+(4-(-2))^2)=sqrt(72)=6sqrt(2)`

`"Radius"=(6sqrt(2))/2=3sqrt(2)`

We now need to find the coordinates of the centre of the circle. These will be the coordinates of the mid point of the diameter.

The coordinate of the mid point of a line are given by:

`(x,y)=>((x_1+x^2)/2,(y_1+y_2)/2)`

`(x,y)=>(h,k)=>((9/2-3/2)/2,(4-2)/2)=(3/2,1)`

So, equation of the circle is:

`(x-3/2)^2+(y-1)^2=(3sqrt(2))^2`

`=>(x-3/2)^2+(y-1)^2=18`

PLOT: