Suppose a circle of radius r is inscribed in a hexagon. What is the perimeter of the hexagon? Thanks!

Question

2489 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-13T22:36:14

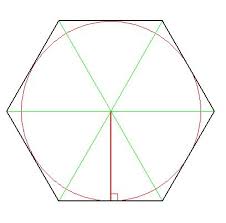
enter image source here

Let length of each side of the regular hexagon circumscribing the circle of radius #r# be #a#.

Then obviously
#(a/2)/r=cot60^@#
#=>a=2rcot60^@=2r*1/sqrt3#.
So perimeter of the hexagon will be #=6a=12/sqrt3r=4sqrt3r#

Suppose a circle of radius r is inscribed in a hexagon. What is the *perimeter* of the hexagon? Thanks!