Suppose A is the arc on the unit circle that connects #(1,0)# to #(-12/13, 5/13)# and passes through #(0,-1)#. Let #u# be the measure of the angle that subtends this arc. Find the value of #sin(u)#?

1 Answer
Somebody N.
Feb 26, 2018

See below.

Explanation:

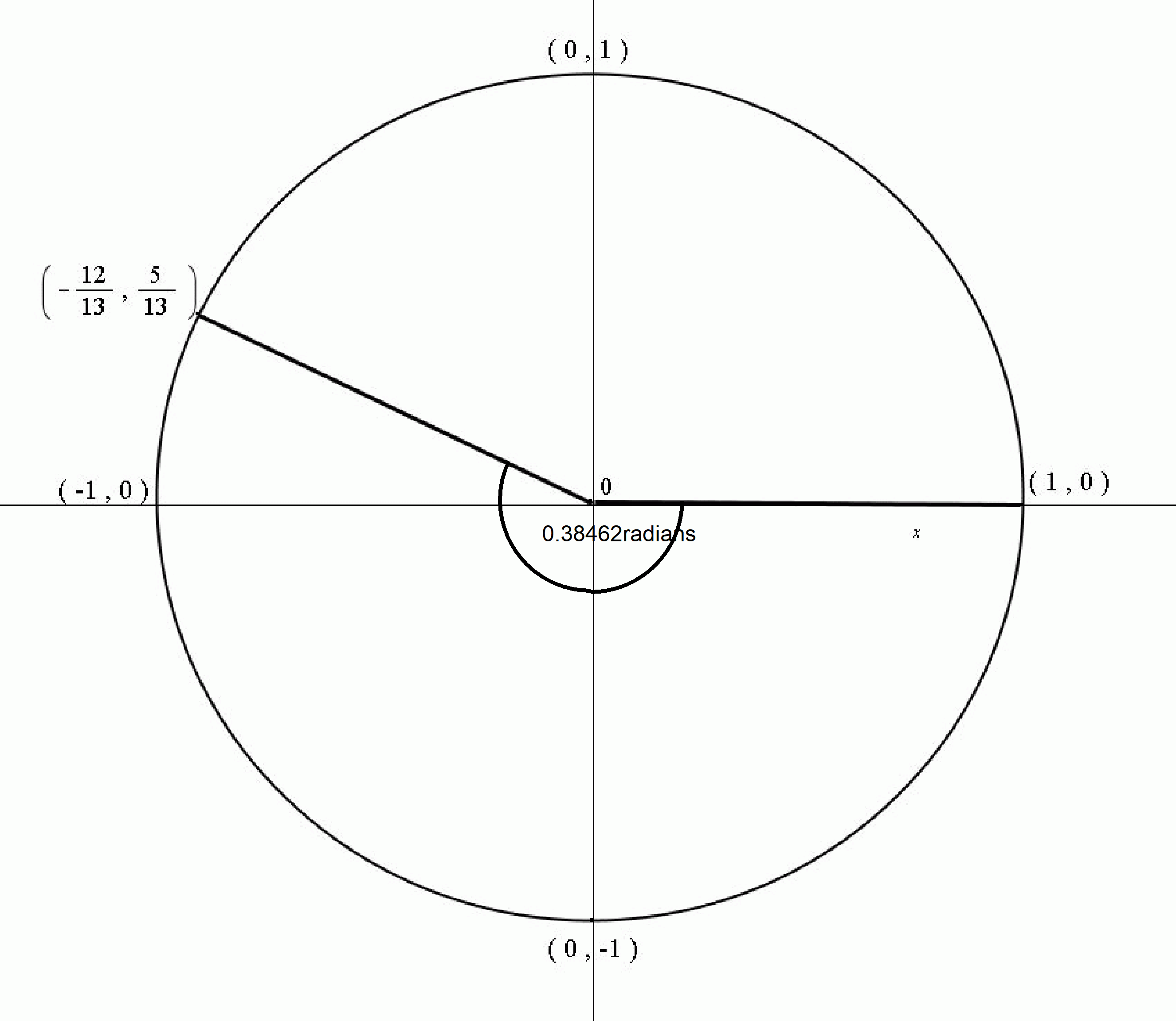
enter image source here

If we pass through point #(0,-1)# then we are rotating in a anti clockwise direction.

We can see by the coordinates #(-12/13,5/13)# that the terminal side is in the II quadrant. The #y# coordinate #5/13# is the sine ratio for the angle that is formed with the negative #x# axis, which will be #arcsin(5/13)#, but we have rotated through the IV and III quadrants, so our angle #bbu# will be #-arcsin(5/13)-pi~~-3.536383774color(white)(8888)#radians or #-202.62^@#.

I have given the angle as a negative rotation, but in angles subtended by arcs this is usually given as a positive angle .i.e. #3.53638377# radians.

#sin(u)=sin(-arcsin(5/13)-pi)~~0.3846153846#

Related questions
Impact of this question
2277 views around the world
You can reuse this answer
Creative Commons License