Suppose ABCD is a rhombus such that the angle bisector of ∠ABD meets AD at point K. Prove that m∠AKB = 3m∠ABK. ?
1 Answer
Mar 12, 2018
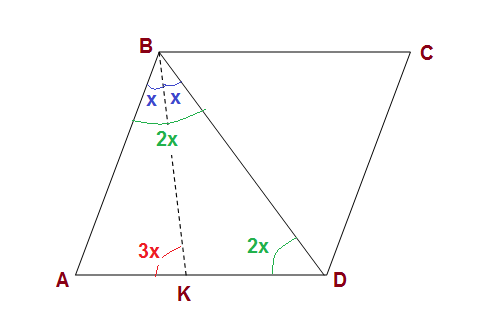 drawn
drawn
Given:
RTP:
Proof:
So
Hence
Now
Hence
Hence

