Suppose that a hole were drilled to the center of the Earth and an evacuated pipe were inserted in the hole. Assume the radius of the Earth is R and the density is uniform with the total mass M. An object of mass m is dropped down the pipe?
Suppose that a hole were drilled to the center of the Earth and an evacuated pipe were inserted in the hole. Assume the radius of the Earth is R and the density is uniform with the total mass M. An object of mass m is dropped down the pipe. Find the velocity of the object when it reaches the center, and the time it takes for the object to reach the center.
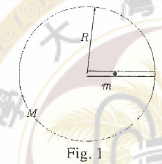
Suppose that a hole were drilled to the center of the Earth and an evacuated pipe were inserted in the hole. Assume the radius of the Earth is R and the density is uniform with the total mass M. An object of mass m is dropped down the pipe. Find the velocity of the object when it reaches the center, and the time it takes for the object to reach the center.

1 Answer
-
Time:
# qquad qquad approx 21 " mins"# -
Velocity:
# qquad approx 7.9 " kps"#
Explanation:
From Gauss' gravity law, gravitational flux is:
Using a spherical Gaussian surface, a concentric sphere of radius
It follows that:
Solving as:
IV's are:
-
#r_o = R# -
#dotr_o = 0#
On arrival at the centre at time
#r = 0 implies omega tau = pi/2 implies tau = pi/2 sqrt( R^3 /(GM)) approx 21 " mins"#
And velocity:

