Suppose that #f# is a linear function such that #f(3) = 6# and #f(-2) = 1#. What is #f(8)#?
2 Answers
Explanation:
Since it's a linear function, it must be of the form
So
Solving for
Therefore, substituting the values of
A lot more explanation is involved than doing the actual maths
Explanation:
Linear basically means 'in line'. This is implying a strait line graph situation
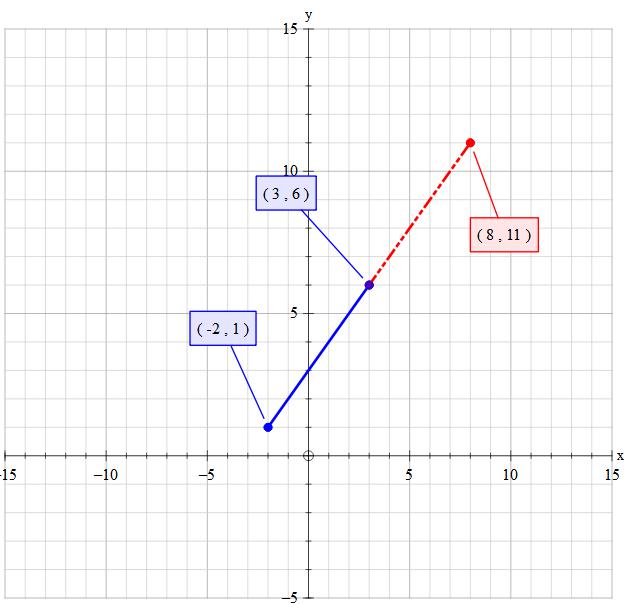
You read left to right on the x-axis so the first value is the least
using:
Set point 1 as
Set point 2 as
Set point 2 as
The gradient (slope) of part will be the same gradient of the whole.
Gradient (slope) is the amount of up or down for a given amount of along, reading left to right.
Thus the gradient gives us:
Thus we have
Multiply both sides by 10
Add 1 to both sides



