Question

Systems of equations help?

`-10x-20y=-20`
`-5x-10y=10`

With work (please!)

Answer 1

The systems of equns.has no solution.`to phi`

Explanation:

Here,

`-10x-20y=-20`

Dividing each term by `(-10)` ,we get

`color(red)(x+2y=2...to(1)`

Also given that,

`-5x-10y=10`

Dividing each term by `(-5)` ,we get

`color(red)(x+2y=-2...to(2)`

Subtracting equn.`(1)` from `(2)`

`x+2y=2`

`x+2y=-2`

`ul(- -color(white)(.........)+`

`color(white)(..............)0=4 to` which is false statement.

Thus, the pair of equn. has no solution.

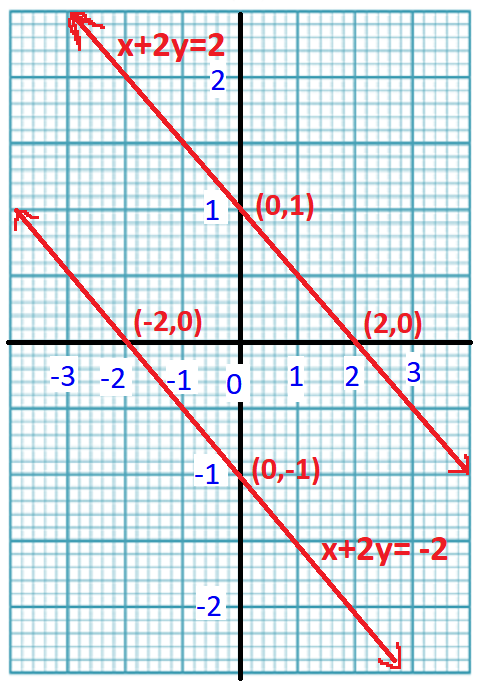
Let us draw the graphs of equn. `(1) and(2)`

From the graph ,we can say that the lines are parallel.

i.e.two lines donot intersect anywhere.

So, the systems of equns.has no solution.

Note:
We know that :If for `a_1,b_1,c_1,a_2,b_2,c_2 in RR`

`a_1x+b_1y+c_1=0 , where,a_1^2+b_1^2!=0`

`a_2x+b_2y+c_2=0 , where,a_2^2+b_2^2!=0 and`

`and a_1/a_2=b_1/b_2!=c_1/c_2=>No color(white)(.)Solution.`

In short, `1/1=2/2!=2/(-2) to phi`